| 题1(单选) |
A、相同
B、可能相等也可能不等
C、单因素方差分析中的Q大
D、无交互作用的双因素方差分析中的Q大
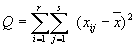 ,它反映所有样本数据的离散程序。
,它反映所有样本数据的离散程序。对于同一批样本数据,其离散程度是一定的,各观察值
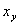 和总平均值
和总平均值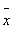 是固定的,因此,不论是用单因素方差分析,还是无交互作用的双因素方差分析,得到的总离差平方和是相同的。
是固定的,因此,不论是用单因素方差分析,还是无交互作用的双因素方差分析,得到的总离差平方和是相同的。此题的关键在于掌握总离差平方和Q的定义。
| 第六章 方差分析 |
|
对于同一批数据,分别进行单因素方差分析和无交互作用的双因素方差分析,问各自分析中的总离差平方和Q的关系( )。 A、相同 B、可能相等也可能不等 C、单因素方差分析中的Q大 D、无交互作用的双因素方差分析中的Q大 |
|
| 解答 | A | |
| 分析 | 总离差平方和Q,即所有观察数据与总平均值的离差平方和,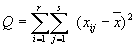 ,它反映所有样本数据的离散程序。 ,它反映所有样本数据的离散程序。对于同一批样本数据,其离散程度是一定的,各观察值 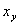 和总平均值 和总平均值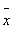 是固定的,因此,不论是用单因素方差分析,还是无交互作用的双因素方差分析,得到的总离差平方和是相同的。 是固定的,因此,不论是用单因素方差分析,还是无交互作用的双因素方差分析,得到的总离差平方和是相同的。此题的关键在于掌握总离差平方和Q的定义。 |
|
|
某单位对全体职工进行满意度调查,让职工对公司的前景进行打分,满分为100分,该单位共有四个部门,现从各部门中随机抽取一些职工,记录其评分见表一。如果各部门职工的评分服从正态分布,而且方差相等,相互独立。在显著性水平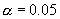 下,检验各部门职工对单位前景的看法有无显著差别? 下,检验各部门职工对单位前景的看法有无显著差别?
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
| 解答 | 假设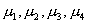 表示四个部门的职工评分的总体平均值。 表示四个部门的职工评分的总体平均值。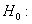  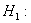 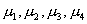 不全相等 不全相等根据样本数据,计算 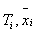 见表二 见表二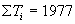 , , 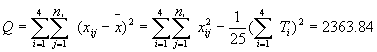 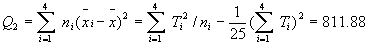 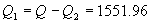 建立方差分析表,见表三 查表知 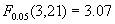 , ,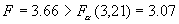
因此拒绝  ,即有95%的把握认为各部门职工对单位前景的看法有显著差异。 ,即有95%的把握认为各部门职工对单位前景的看法有显著差异。
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
| 分析 | 要掌握方差分析的具体步骤,熟悉方差分析表及各计算公式,从而能熟练运用方差分析技术解决具体问题。 表一:
表二:
表三:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||