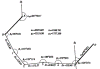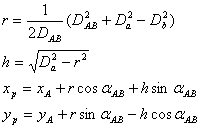第6章 小地区控制测量
本章提要
本章主要讲述控制测量的原理及方法。重点介绍导线测量、小三角测量原理和平差计算方法;三、四等水准测量和三角高程测量原理及方法。
§6.1 控制测量概述
测绘的基本工作是确定地面上地物和地貌特征点的位置,即确定空间点的三维坐标。这样的工作若从一个原点开始,逐步依据前一个点测定后一个点的位置,必然会将前一个点的误差带到后一个点上。这样测量方法误差逐步积累,将会达到惊人的程度。所以,为了保证所测点位的精度,减少误差积累,测量工作必须遵循“从整体到局部”、“由高级到低级”、“先整体后碎部”的组织原则。为此,必须首先建立控制网,然后根据控制网进行碎步测量和测设。由在测区内所选定的若干个控制点所构成的几何图形,称为控制网。
控制网分为平面控制网和高程控制网两种。测定控制点平面位置(x、y)的工作称分为平面控制测量,测定控制点高程(H)的工作称为高程控制测量。
在全国范围内建立的控制网,称为国家控制网。它是全国各种比例尺测图的基本控制网,并为确定地球的形状和大小提供研究资料。国家控制网是用精密测量仪器和方法依照施测精度安一、二、三、四共四个等级建立的,其低级点受高级点逐级控制。
6.1.1 平面控制测量
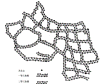
平面控制测量是确定控制点的平面位置。建立平面控制网的经典方法有三角测量和导线测量。如图6-1中,A、B、C、D、E、F组成互相邻接的三角形,观测所有三角形的内角,并至少测量其中一条边长作为起算边,通过计算就可以获得它们之间的相对位置。这种三角形的顶点称为三角点,构成的网形称为三角网,进行这种控制测量称为三角测量。
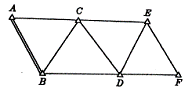
图6-1 三角网
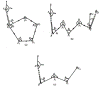
又如图6—2中控制点1、2、3…用折线连接起来,测量各边的长度和各转折角,通过计算同样可以获得它们之间的相对位置。这种控制点称为导线点,进行这种控制测量称为导线测量。
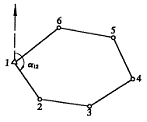
图6-2 导线网
平面控制网除了经典的三角测量和导线测量外,还有卫星大地测量。目前常用的是GPS卫星定位。见6-3,在A、B、C、D控制点上,同时接收GPS卫星![]() 、
、![]() 、
、![]() 、
、![]() …发射的无线电信号,从而确定地面点位,称为GPS控制测量。
…发射的无线电信号,从而确定地面点位,称为GPS控制测量。
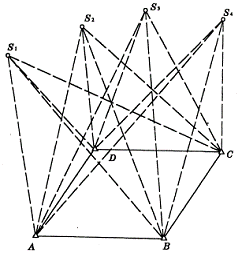
图6-3 GPS网
国家平面控制网,是在全国范围内建立的控制网。它是全国各种比例尺测图和工程建设的基本控制网,也为空间科学技术和军事提供精确的点位坐标、距离、方位资料,并为研究地球大小和形状、地震预报等提供重要资料。逐级控制,分为一、二、三、四等三角测量和精密导线测量。图6-4为部分地区国家一、二等三角控制网的示意图。
图6-4 部分地区国家一、二等三角网示意图
城市控制测量是为大比例尺地形测量建立控制网,作为城市规划、施工放样的测量依据。城市平面控制网一般可分为二、三、四等三角网及一、二级小三角网或一、二、三级导线。然后再布设图根小三角网或图根导线。按1985年城市测量规范,其技术要求列于表6-l和表6-2。
城市三角网及图根三角网的主要技术要求 表6-1
|
等级 |
测角中误差(″) |
三角形最大闭合差(″) |
平均边长 (km) |
起始边相对中误差 |
最弱边相对中误差 |
测回数 |
||
|
DJ1 |
DJ2 |
DJ3 |
||||||
|
二等 |
±1.0 |
±3.5 |
9 |
1:30万 |
1:12万 |
12 |
|
|
|
三等 |
±1.8 |
±7.0 |
5 |
首级1:20万 |
1:8万 |
6 |
9 |
|
|
四等 |
±2.5 |
±9.0 |
2 |
首级1:12万 |
1:4.5万 |
4 |
6 |
|
|
一级 |
±5 |
±15 |
1 |
1:4万 |
1:2万 |
|
2 |
6 |
|
二级 |
±10 |
±30 |
0.5 |
1:2万 |
1:1万 |
|
1 |
2 |
|
图根 |
±20 |
±60 |
不大于测图最大视距1.7倍 |
1:1万 |
|
|
|
1 |
城市导线及图根导线的主要技术要求 表6-2
|
等级 |
测角中误差 (″) |
方向角闭合差(″) |
附合导线长度(km) |
平均边长 (m) |
测距中误差 (mm) |
全长相对中误差 |
|
一级 |
±5 |
|
3.6 |
300 |
±15 |
1:1.4万 |
|
二级 |
±8 |
|
2.4 |
200 |
±15 |
1:1万 |
|
三级 |
±12 |
|
1.5 |
120 |
±15 |
1:0.6万 |
|
图根 |
±30 |
|
|
|
|
1:0.2万 |
注:n为测站数。
随着科学技术的发展和现代化测量仪器的出现,三角测量这一传统定位技术大部分已被卫星定位技术所替代。1992年国家制定的《GPS控制测量规范》将GPS控制网分成A~E五级,见表6-3。其中A、B相当于国家一、二等三角点,C、D相当于城市三、四等。我国已于1992年在全国布设了覆盖全国的A级GPS网点27个,1996年完成了全国B级GPS网点730个,城市控制网也基本采用GPS定位技术。
GRS控制网主要技术要求 表6-3
|
|
A |
B |
C |
D |
E |
|
固定误差a(mm) 比例误差系数b(10 相邻点最小距离(km) 相邻点最大距离(km) 相邻点平均距离(km) |
≤5 ≤0.1 100 ]200 300 |
≤8 ≤1 15 250 70 |
≤10 ≤5 5 40 15~10 |
≤10 ≤10 2 15 10~5 |
≤10 ≤20 1 10 5~2 |
6.1.2 高程控制网
建立高程控制网的主要方法是水准测量。在山区也可以采用三角高程测量的方法来建立高程控制网,这种方法不受地形起伏的影响,工作速度快.但其精度较水准测量低。
国家水准测量分为一、二、三、四等,逐级布设.一、二等水准测量是用高精度水准仪和精密水准测量方法进行施测,其成果作为全国范围的高程控制之用。三、四等水准测量除用于国家高程控制网的加密外,在小地区用作建立首级高程控制网。
为了城市建设的需要所建立的高程控制称为城市水准测量,采用二、三、四等水准测量及直接为测地形图用的图根水准测量,其技术要求列于表6-4。
城市与图根水准测量的主要技术要求(mm) 表6-4
(点击图片放大)注:①
![]() 为测段、区段或路线长度,L为附合路线或环线长度,
为测段、区段或路线长度,L为附合路线或环线长度,![]() 为检测测段长度,均以千米计。
为检测测段长度,均以千米计。
②山区是指路线中最大高差超过400m的地区.
在平原地区,可采用GPS水准进行四等水准测量。在地形比较复杂或地质构造复杂的地区,采用GPS水准时,需进行高程异常改正。
§6.2 直线定向及坐标正反算
6.2.1 直线定向的概念
确定一条直线的方向称为直线定向。进行直线定向,首先要选定一个标准方向线,作为直线定向的依据。
在测量中常以真子午线或磁子午线作为基本方向。真子午线的方向用天文测量的方法测定,或用陀螺经纬仪方法测定。磁子午线可用罗盘仪测定。
由于地球磁极与地球旋转轴南北极不重合,因此过地球上某点的真子午线与磁子午线不重合。两者之间的夹角称为磁偏角,用![]() 表示,见图6—5。
表示,见图6—5。
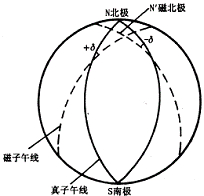
图6-5 真子午线与磁子午线
磁子午线北端偏于真子午线以东为东偏(+![]() ),偏于真子午线以西为西偏(-
),偏于真子午线以西为西偏(-![]() )。地球上不同地点磁偏角也不同。
)。地球上不同地点磁偏角也不同。
我国磁偏角的变化大约在+6°~-10°之间。北京地区磁偏角为西偏,约-5°左右。地球磁极是不断变化的,北磁极正以每年l0k的速度向地理北极移动。由于磁极变化,磁偏角也在变化。此外,罗盘仪还会受到地磁场及磁暴的影响。所以测量中一般用真子午线作为基本方向线。只有在施测困难的地区,精度要求不高的地区,如森林勘测中用磁子午线。
地面上不同经度的子午线收敛于两极。地面上两点子午线方向的夹角称为子午线收敛角,用![]() 表示,见图6-6。
表示,见图6-6。
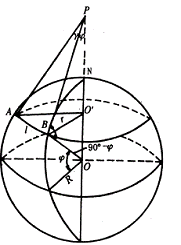
图6-6 子午线收敛角
设A、B为同纬度上的两点,其距离为![]() 。过A、B两点分别作子午线的切线交于地轴P点。AP、BP为子午线方向。若A、B相距不太远时,子午线收敛角
。过A、B两点分别作子午线的切线交于地轴P点。AP、BP为子午线方向。若A、B相距不太远时,子午线收敛角![]() 可用下式计算:
可用下式计算:
![]() (6-1)
(6-1)
在直角三角形BOP中,![]() ,代入上式得:
,代入上式得:
![]() (6-2)
(6-2)
从上式可见,纬度愈低,子午线收敛角愈小,在赤道上为零。纬度越高,收敛角愈大。
6.2.2 直线定向方法
测量中常用方位角表示直线方向。从标准方向的北端起,顺时针方向到某直线的水平夹角,称为该直线的方位角,见图6-7。方位角值从0°~360°。
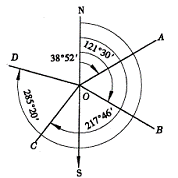
图6-7方位角
(1)真方位角和磁方位角
若标准方向为真子午线方向,则称真方位角,用A表示。若标准方向为磁子午线方向,则称磁方位角,用![]() 表示。真方位角和磁方位角之间的关系为:
表示。真方位角和磁方位角之间的关系为:
![]() (6-3)
(6-3)
(2)坐标方位角
在测量中常采用高斯—克吕格坐标纵轴为基本方向,从纵坐标轴的北端按顺时针方向到一直线的水平角为该直线的坐标方位角,或称为方位角。用![]() 表示。
表示。
(3)正、反方位角
同一条直线在不同端点量测,其方位角也不同。测量中常把直线前进方向称为正方向,反之称为反方向。如图6-8,设A为AB直线的起端,B为终端,则![]() 为正真方位角,
为正真方位角,![]() 为反真方位角。
为反真方位角。
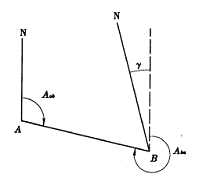
图6-8 正、反方位角
正、反真方位角之间的关系为:
![]() =
=![]() (6-4)
(6-4)
式中![]() 的正负号为:直线位于中央子午线以东,
的正负号为:直线位于中央子午线以东,![]() 为正;以西为负。
为正;以西为负。
由于一条直线的正、反坐标方位角无子午线收敛角,所以为:
![]() =
=![]() (6-5)
(6-5)
6.2.3 坐标方位角的推算
在测量中为了使测量成果坐标统一,并能保证测量精度,常将线段首尾连接成折线,并与已知边AB相连。若AB边的坐标方位角![]() 已知,又测定了AB边和B1边的水平角
已知,又测定了AB边和B1边的水平角![]() (称为连接角)和各点的转折角
(称为连接角)和各点的转折角![]() 、
、![]() 、
、![]() ,利用正、反方位角的关系和测定的转折角可以推算连续折线上各线段的坐标方位角(见图6—9)如下:
,利用正、反方位角的关系和测定的转折角可以推算连续折线上各线段的坐标方位角(见图6—9)如下:
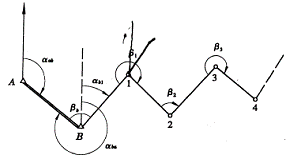
图6-9 方位角计算
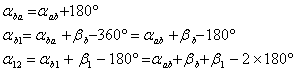
![]() (6-6)
(6-6)
上式中![]() 是折线推算前进方向的左角。若测定的是右角则用下式计算
是折线推算前进方向的左角。若测定的是右角则用下式计算
![]() (6-7)
(6-7)
6.2.4 坐标正、反算
(1)坐标正算公式
已知边长和方位角,由已知点计算待定点的坐标,称为坐标正算。
如图6—10,A为已知点,其坐标为![]() ,A到待定点B的边长为
,A到待定点B的边长为![]() (平距),方位角为
(平距),方位角为![]() 。则B点坐标为:
。则B点坐标为:
![]() (6-8)
(6-8)
式中:![]() 、
、![]() —坐标增量。
—坐标增量。
(2)坐标反算公式:
已知两点坐标,反求边长和方位角,称为坐标反算(如图6—10)。
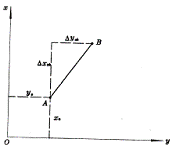
图6-10 坐标计算
方位角公式为:
![]() (6-9)
(6-9)
边长计算公式为:
![]() (6-10)
(6-10)
注意,用式(6-9)计算的角是象限角(R),还应根据方位角与象限角的关系,将象限角换算成方位角。由于测量采用的坐标定义与数学中的笛卡尔坐标不一样,所以象限定义也不同,见图6-11。坐标方位角和象限角的关系见表6-5 。
方位角和象限角的关系 表6-5
|
象限 |
由方位角换算象限角 |
由象限角换算方位角 |
|
象限Ⅰ |
R=α |
α=R |
|
象限Ⅱ |
R=180°-α |
α=180°-R |
|
象限Ⅲ |
R=α-180° |
α=180°+R |
|
象限Ⅳ |
R=360°-α |
α=360°-R |
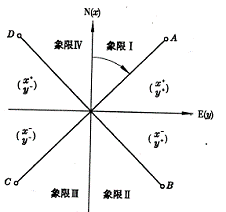
图6-11 象限角
§6.3 导线测量
导线测量布设灵活,要求通视方向少,边长可直接测定,适宜布设在视野不够开阔的地区,如城市、厂区、矿山建筑区、森林等,也适用于狭长地带的控制测量,如铁路、隧道、渠道等。随着全站仪的普及,一测站可同时完成测距、测角,导线测量方法广泛地用于控制网的建立,特别是图根导线的建立。
导线测量的布设形式有以下几种:
图6-12 导线的基本形式
(1)闭合导线
导线的起点和终点为同一个已知点,形成闭合多边形,如图6-12(a),B点为已知点,![]() 、…、
、…、![]() 为待测点,
为待测点,![]() 为已知方向。
为已知方向。
(2)附合导线
敷设在两个已知点之间的导线称为附合导线。如图6-12(b),B点为已知点,![]() 为已知方向,经过
为已知方向,经过![]() 点最后附合到已知点C和已知方向
点最后附合到已知点C和已知方向![]() 。
。
(3)支导线
从一个已知点出发不回到原点,也不附合到另外已知点的导线称为支导线,支导线也称自由导线,如图6-12(c)。由于支导线无法检核,故布设时应十分仔细,规范规定支导线不得超过三条边。
6.3.1 导线测量外业工作
导线测量外业工作包括踏勘选点、角度测量、边长测量。
(1)踏勘选点
在踏勘选点前应尽量搜集测区的有关资料,如地形图、已有控制点的坐标和高程,及控制点点之记。在图上规划导线布设方案,然后到现场选点,埋标志。
选点注意事项:
①导线点应选在土质坚硬,能长期保存和便于观测的地方。
②相邻导线点间通视良好,便于测角、量边。
③导线点视野开阔,便于测绘周围地物和地貌。
④导线边长应大致相等,避免过长、过短,相邻边长之比不应超过三倍。
导线点选定后,应在地面上建立标志,并沿导线走向顺序编号,绘制导线略图。对等级导线点应按规范埋设混凝土桩,见图6-13(a),并在导线点附近的明显地物(房角、电杆)上用油漆注明导线点编号和距离,并绘制草图,注明尺寸,称为点之记,见图6-13(b)。
图6-13 混凝土桩及点之记
(2)外业测量
①边长测量
导线边长常用电磁波测距仪测定。由于测的是斜距,因此要同时测竖直角,进行平距改正。图根导线也可采用钢尺量距。往返丈量的相对精度不得低于1/3000,特殊困难地区允许1/1000,并进行倾斜改正。
②角度测量
导线角度测量有转折角测量和连接角测量。在各待定点上所测的角为转折角,这一工作称为转折角测量,如图6-12中![]() ~
~![]() 。这些角分为左角和右角。在导线前进方向右侧的水平角为右角,如图6-12(a);左侧的为左角,如图6—12(b)。对角度测量精度的要求见表6-2。导线应与高级控制点连测,才能得到起始方位角,这一工作称为连接角测量,也称导线定向。目的是使导线点坐标纳入国家坐标系统或该地区统一坐标系统。附合导线与两个已知点连接,应测两个连接角
。这些角分为左角和右角。在导线前进方向右侧的水平角为右角,如图6-12(a);左侧的为左角,如图6—12(b)。对角度测量精度的要求见表6-2。导线应与高级控制点连测,才能得到起始方位角,这一工作称为连接角测量,也称导线定向。目的是使导线点坐标纳入国家坐标系统或该地区统一坐标系统。附合导线与两个已知点连接,应测两个连接角![]() 、
、![]() 。闭合导线和支导线只需测一个连接角
。闭合导线和支导线只需测一个连接角![]() ,见图6-12。对于独立地区周围无高级控制点时,可假定某点坐标,用罗盘仪测定起始边的磁方位角作为起算数据。
,见图6-12。对于独立地区周围无高级控制点时,可假定某点坐标,用罗盘仪测定起始边的磁方位角作为起算数据。
6.3.2 导线测量内业计算
导线内业计算之前,应全面检查导线外业工作记录及成果是否符合精度要求。然后绘制导线略图,注上实测边长、转折角、连接角和起始坐标,以便于导线坐标计算,见图6-14 。
图6-14 符合导线
(1)附合导线计算
由于附合导线是在两个已知点上布设的导线,因此测量成果应满足两个几何条件。
a.方位角闭合条件:即从已知方位角![]() ,通过各
,通过各![]() 角推算出CD边方位角
角推算出CD边方位角![]() ,应与已知方位角
,应与已知方位角![]() —致。
—致。
b.坐标增量闭合条件:即从B点已知坐标![]() ,经各边长和方位角推算求得的C点坐标
,经各边长和方位角推算求得的C点坐标![]() 、
、![]() 应与已知C点坐标
应与已知C点坐标![]() 、
、![]() 一致。
一致。
上述两个条件是附合导线外业观测成果检核条件,又是导线坐标计算平差的基础。其计算步骤如下:
①坐标方位角的计算与角度闭合差的调整
根据式(6-6),推算CD边坐标方位角为:
![]() (6-11)
(6-11)
由于测角存在误差,所以![]() 和
和![]() 有差,称为角度闭合差:
有差,称为角度闭合差:
![]() (6-12)
(6-12)
本例中![]() ,则
,则![]() 。
。
根据表6-2,图根导线角度闭合差容许误差为:
![]()
若![]() ≥
≥![]() ,说明角度测量误差超限,要重新测角;若
,说明角度测量误差超限,要重新测角;若![]() <
<![]() ,则只需对各角度进行调整。由于各角度是同精度观测,所以将角度闭合差反符号平均分配给各角,然后再计算各边方位角。最后以计算的
,则只需对各角度进行调整。由于各角度是同精度观测,所以将角度闭合差反符号平均分配给各角,然后再计算各边方位角。最后以计算的![]() 和
和![]() 是否相等作为检核。
是否相等作为检核。
②坐标增量闭合差的计算与调整
利用上述计算的各边坐标方位角和边长,可以计算各边的坐标增量。各边坐标增量之和理论上应与控制点B、C的坐标差一致,若不一致,产生的误差称为坐标增量闭合差![]() 、
、![]() 。计算式为:
。计算式为:
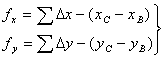 (6-13)
(6-13)
由于![]() 、
、![]() 的存在,使计算出的C′点与C点不重合,见图6-15。
的存在,使计算出的C′点与C点不重合,见图6-15。
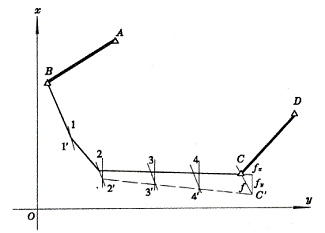
图6-15 导线全长闭合差
CC′用![]() 表示,称为导线全长闭合差,用下式表示:
表示,称为导线全长闭合差,用下式表示:
![]() (6-14)
(6-14)
![]() 值和导线全长
值和导线全长![]() 之比K称为导线全长相对闭合差,即:
之比K称为导线全长相对闭合差,即:
![]() (6-15)
(6-15)
K值的大小反映了测角和测边的综合精度。不同导线的相对闭合差容许值不同,见表6-2。图根导线K值小于1:2000,困难地区K值可放宽到1:1000。
一般情况下是量距有误差。若![]() 应分析原因,必要时重测。当
应分析原因,必要时重测。当![]() 值符合精度要求,可以进行坐标增量调整。
值符合精度要求,可以进行坐标增量调整。
本例中![]()
![]()
![]() ≤
≤![]()
调整的方法是将![]() 、
、![]() 反号按与边长成正比的原则进行分配,对于第
反号按与边长成正比的原则进行分配,对于第![]() 边的坐标增量改正值为:
边的坐标增量改正值为:
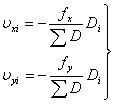 (6-16)
(6-16)
计算完毕,改正后的坐标增量之和应与B、C两点坐标差相等,以此作为检核。
③坐标计算
根据起始点B的坐标及改正后各边的坐标增量按下式计算各点坐标:
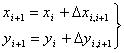
最后推算出的C′点坐标应与原来C点坐标一致。
附合导线计算可列表格计算,见表6-6。
附合导线计算表 表6-6
闭合导线计算方法与附合导线相同,也要满足角度闭合条件和坐标闭合条件。
①角度闭合差的计算与调整
闭合导线测的是内角,所以角度闭合条件是要满足n多边形内角和条件:
![]()
角度闭合差
![]() (6-18)
(6-18)
②坐标增量闭合差的计算与调整
闭合导线的起、终点是一个点,所以坐标增量理论值为零。坐标增量闭合差为:
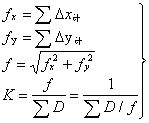 (6-19)
(6-19)
角度闭合差![]() ,坐标增量闭合差
,坐标增量闭合差![]() 、
、![]() 及导线全长闭合差
及导线全长闭合差![]() 的检验和调整同附合导线。由起点坐标通过各点坐标增量改正计算,求定各点坐标,最后推回到1点坐标应相同,作为计算检核。表6-7为图6-16的闭合导线计算表。
的检验和调整同附合导线。由起点坐标通过各点坐标增量改正计算,求定各点坐标,最后推回到1点坐标应相同,作为计算检核。表6-7为图6-16的闭合导线计算表。
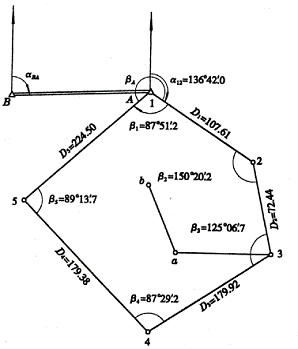
图6-16 闭合导线°′
闭合导线坐标计算表 表6-7
§6.4 小三角测量
小三角测量与导线测量相比,量边工作量大为减少。所以在山区、丘陵和城市首级控制网大多采用小三角测量建立平面控制网。三角网常用的基本图形有单三角锁、中点多边形、大地四边形、线形锁等,如图6—17所示。本节只介绍单三角锁测量。
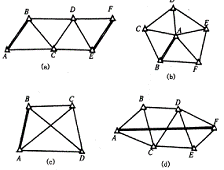
(a)单三角锁;(b)中点多边形;(c)大地四边形;(d)线形锁
图6-17 小三角网的基本图形
6.4.1 小三角测量作业
小三角测量外业工作包括踏勘选点、角度测量和基线边测量。
(1)选点、建立标志
同导线测量,选点前要搜集测区已有的地形图和控制点成果,在图上初步拟定布网方案,再到实地踏勘、选点。
选点应注意以下几点:
①基线应选在地势平坦,便于量距的地方(用电磁波测距仪测基线,不受此限制)
②三角点应选在地势较高、土质坚实的地方,相邻三角点应互相通视。
③为保证推算边长的精度,三角形内角一般不应小于30°,不大于120°。
小三角点选定后,同导线测量一样应在地面上埋标志,绘制点之记。
(2)角度测量
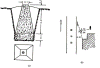
角度测量是小三角测量的主要外业工作。有关技术指标见表6-1。三角点照准标志一般用花杆或小标杆,底部对准三角点标志中心,标杆用杆架或三根铅丝拉紧,并保证拉杆垂直。当边长较短时,可用三个支架悬挂垂球,在垂球线上系一小花杆作照准标志,见图6—18。
在三角点上,当观测方向是两个时,采用测回法测角;当观测方向为三个或三个以上时,采用全圆测回法。具体测量方法见第3章。
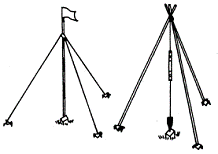
图6-18 小三角点照准标志
角度测量时应随时计算各三角形角度闭合差![]() ,公式为
,公式为
![]()
式中:![]() -三角形序号。
-三角形序号。
若![]() 超出表6-1的规定,应重测。角度观测结束后,按菲列罗公式计算测角中误差
超出表6-1的规定,应重测。角度观测结束后,按菲列罗公式计算测角中误差![]() :
:
![]() (6-21)
(6-21)
(3)基线测量
一般采用电磁波测距测量三角网起始边的平距。若采用钢尺丈量时,要用精密丈量方法。
6.4.2 小三角测量内业计算
小三角测量内业计算包括外业成果的整理、检查,三角测量成果平差计算,边长和坐标计算。一般图根小三角测量计算采用近似平差,一、二级小三角测量用严密平差。下面主要介绍图根三解锁的近似平差计算方法。
(1)绘制小三角测量略图
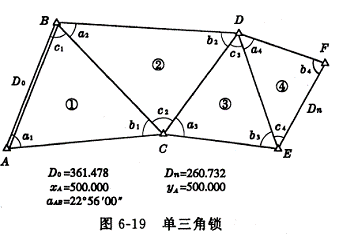
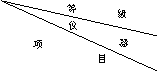
图6-19为单三角锁略图。图中![]() 或
或![]() 是起始边。从第一个三角形开始,由
是起始边。从第一个三角形开始,由![]() 按三角形正弦定律推算与下一个三角形共用边的边长,此时该边长即为第二个三角形的已知边。依次类推,即可推出所有三角形的边长。为了方便,三角形内角按以下规定编号:已知边所对的角为
按三角形正弦定律推算与下一个三角形共用边的边长,此时该边长即为第二个三角形的已知边。依次类推,即可推出所有三角形的边长。为了方便,三角形内角按以下规定编号:已知边所对的角为![]() ,待求边所对的角为
,待求边所对的角为![]() ,第三边所对的角为
,第三边所对的角为![]() 。
。![]() 、
、![]() 称为传距角,
称为传距角,![]() 称为间隔角。
称为间隔角。
(2)角度闭合差的计算与调整
设![]() 为第
为第![]() 个三角形的角度观测值,则各三角形的角度闭合差用式(6-18)计算,图根小三角角度闭合差容许值
个三角形的角度观测值,则各三角形的角度闭合差用式(6-18)计算,图根小三角角度闭合差容许值![]() ≤60″。若
≤60″。若![]() ≤
≤![]() ,则进行角度闭合差调整。
,则进行角度闭合差调整。
设各角度第一次改正数为![]() 。因各角度为同精度观测,各改正数应相等。故改正数为:
。因各角度为同精度观测,各改正数应相等。故改正数为:
![]() (6-22)
(6-22)
改正值取至秒位。第一次改正后的角值为:
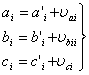 (6-23)
(6-23)
经过第一次改正后的角度应满足三角形闭合条件,即:
![]() (6-24)
(6-24)
(3)基线闭合差的计算与调整
根据基线![]() 和第一次改正后的角值
和第一次改正后的角值![]() 、
、![]() 按正弦定理推算另一条基线
按正弦定理推算另一条基线![]() 。
。
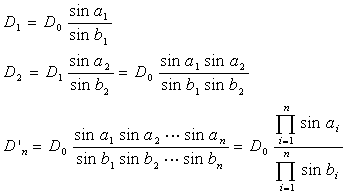
式中![]() 为连乘符号。
为连乘符号。
计算的第二条基线![]() 应与实测的
应与实测的![]() 相等。但由于第一次改正后的角度仍有误差,所以往往
相等。但由于第一次改正后的角度仍有误差,所以往往![]()
![]()
![]() ,从而产生基线闭合差
,从而产生基线闭合差![]() 。
。
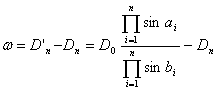 (6-25)
(6-25)
为了消除![]() 误差,须对
误差,须对![]() 、
、![]() 进行第二次改正。设
进行第二次改正。设![]() 为角度第二次改正数,则
为角度第二次改正数,则
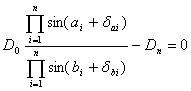 (6-26)
(6-26)
将式(6-26)按台劳级数展开,取前两项,得:
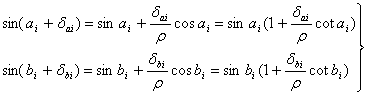 (6-27)
(6-27)
将式(6-27)代入式(6-26),得:
由于![]() 很小,所以有
很小,所以有
![]()
将上式代入式(6-28),得:
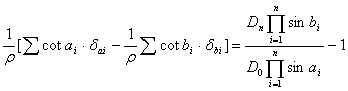
为使第二次改正后仍能满足三角形内角之和为180°,必使![]() 与
与![]() 大小相等,符号相反,所以令
大小相等,符号相反,所以令![]()
基线闭合差为:
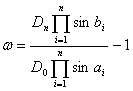 (6-30)
(6-30)
则
![]() (6-31)
(6-31)
第二次改正后的角度值![]() 为:
为:
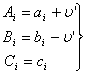 (6-32)
(6-32)
(4)边长和坐标计算
根据第二次改正后的角度和基线![]() ,按正弦定理计算三角形各边长。最后求得的
,按正弦定理计算三角形各边长。最后求得的![]() 应与
应与![]() 相等。
相等。
求得各边长和改正后的角度,按闭合导线计算各点坐标。
以图6-19为例,按上述推算步骤,角度和边长计算见表6-8,坐标计算见表6-9,表中坐标计算按A-C-E-F-D-B-A闭合导线进行。
三角锁闭合差调整与边长计算表 表6-8
|
三角形 |
角号 |
角度观测值 ( °′″) |
第一次改正(″) |
第一次改正后角度( °′″) |
|
第二次改正(″) |
第二次改正后角度 ( °′″) |
边长 (m) |
|
1 |
|
63 41 18 51 13 44 65 04 48 |
+3 +3 +4 |
63 41 21 51 13 47 65 04 52 |
+0.49 +0.80 |
+2 -2 |
61 41 23 51 13 45 65 04 52 |
415.607 361.478 420.475 |
|
|
179 59 50 |
|
180 00 00 |
180 00 00 |
||||
|
2 |
|
41 05 39 58 16 12 80 38 15 |
-2 -2 -2 |
41 05 37 58 16 10 80 38 13 |
+1.15 +0.62 |
+2 -2 |
41 05 39 58 16 08 80 38 13 |
321.188 415.607 482.138 |
|
|
180 00 06 |
|
180 00 00 |
180 00 00 |
||||
|
3 |
|
60 08 24 63 07 34 56 43 50
|
+4 +4 +4 |
60 08 28 63 07 38 56 43 54 |
+0.57 +0.51 |
+2 -2 |
60 08 30 63 07 36 56 43 54 |
312.276 321.188 301.061 |
|
|
179 59 48 |
|
180 00 00 |
180 00 00 |
||||
|
4 |
|
53 59 25 75 39 28 50 21 16 |
-3 -3 -3 |
53 59 22 75 39 25 50 21 13 |
+0.73 +0.26 |
+2 -2 |
53 59 24 75 39 23 50 21 13 |
260.732 312.276 248.188 |
|
|
180 00 09 |
|
180 00 00 |
180 00 00 |
||||
|
|
|
|
|
|
+5.13 |
|
|
|
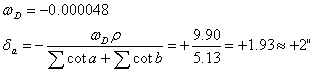
![]()
三角锁坐标计算表 表6-9
|
三角点 |
转折角(左角) ( °′″) |
转方位角 ( °′″) |
边长D (m) |
坐标增量(m) |
坐标 (m) |
三角点 |
||
|
|
|
|
|
|||||
|
B |
|
22 56 00 |
|
|
|
|
|
|
|
A |
63 41 23 |
86 37 23 |
420.475 |
+24.768 |
+419.745 |
500.000 |
500.000 |
A |
|
C |
192 00 28 |
98 37 51 |
301.061 |
-45.180 |
+297.652 |
524.768 |
919.745 |
C |
|
E |
113 28 49 |
32 06 40 |
260.732 |
+220.845 |
+138.595 |
479.588 |
1217.397 |
E |
|
F |
75 39 23 |
287 46 03 |
248.189 |
+75.736 |
-236.351 |
700.433 |
1355.992 |
F |
|
D |
168 59 26 |
276 45 29 |
482.138 |
+56.737 |
-478.788 |
776.169 |
1119.641 |
D |
|
B |
106 10 31 |
22 56 00 |
361.478 |
-332.906 |
-140.853 |
832.906 |
640.853 |
B |
|
A |
|
|
|
|
|
500.000 |
500.000 |
A |
§6.5 交会定点
当原有控制点不能满足工程需要时,可用交会法加密控制点,称为交会定点。常用的交会法有前方交会、后方交会和距离交会。
6.5.1 前方交会
如图6-20(a),在已知点A、B处分别对P点观测了水平角![]() 和
和![]() ,求P点坐标,称为前方交会。为了检核和提高P点精度,通常需从三个已知点A、B、C分别向P点观测水平角,如图 6-20(b),分别由两个三角形计算P点坐标。
,求P点坐标,称为前方交会。为了检核和提高P点精度,通常需从三个已知点A、B、C分别向P点观测水平角,如图 6-20(b),分别由两个三角形计算P点坐标。
现以一个三角形为例说明前方交会的定点方法。
(1)根据已知点A、B坐标分别为(![]() )和(
)和(![]() )计算已知边AB的方位角和边长为:
)计算已知边AB的方位角和边长为:
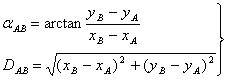 (6-33)
(6-33)
(2)在A、B两点设站,测出水平角![]() ,再推算AP和BP边的坐标方位角和边长
,再推算AP和BP边的坐标方位角和边长
由图6-20a得:
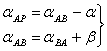 (6-34)
(6-34)
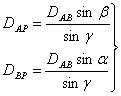 (6-35)
(6-35)
式中:
![]() (6-36)
(6-36)
(3)最后计算P点坐标
分别由A点和B点按下式推算P点坐标,并校核。
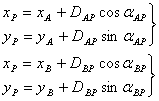 (6-37)
(6-37)
下面介绍一种应用A、B坐标(![]() )和(
)和(![]() )和在A、B两点设站,测出的水平角
)和在A、B两点设站,测出的水平角![]() 直接计算P点坐标的公式,公式推导从略。
直接计算P点坐标的公式,公式推导从略。
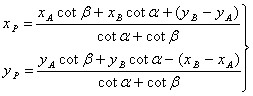 (6-38)
(6-38)
应用式(6-38)时,可以直接利用计算器,但要注意A、B、P的点号须按反时针次序排列(见图6-20)。
前方交会计算见表6-10。
前方交会计算表 表6-10
6.5.2 后方交会
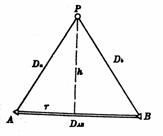
图6-21中A、B、C为已知点,将经纬仪安置在P点上,观测P点至A、B、C各方向的夹角![]() 。根据已知点坐标,即可推算P点坐标,这种方法称为后方交会。其优点是不必在多个点上设站观测,野外工作量少,故当已知点不易到达时,可采用后方交会法确定待定点。后方交会法计算工作量大,计算公式很多,这里仅介绍其中一种计算方法——全切公式法。
。根据已知点坐标,即可推算P点坐标,这种方法称为后方交会。其优点是不必在多个点上设站观测,野外工作量少,故当已知点不易到达时,可采用后方交会法确定待定点。后方交会法计算工作量大,计算公式很多,这里仅介绍其中一种计算方法——全切公式法。
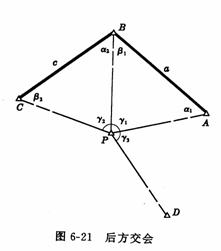
下面介绍具体定点方法:
(1) 根据已知点A、B、C的坐标(![]() )和(
)和(![]() ),利用坐标反算公式计算AB、BC坐标方位角
),利用坐标反算公式计算AB、BC坐标方位角![]() 和边长
和边长![]() 。
。
(2)计算![]() 。
。
从图6-21中可见:
![]()
又因
![]() (6-39)
(6-39)
所以
![]() (6-40)
(6-40)
在ΔAPB和ΔBPC中,根据正弦定理可得:
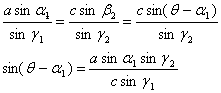
经过整理可得:
![]() (6-41)
(6-41)
根据式(6-40)和式(6-41)可解出![]() 、
、![]() 。
。
(3)计算![]() 和
和![]()
![]() (6-42)
(6-42)
![]() (6-43)
(6-43)
利用![]() 和
和![]() 之和应等于
之和应等于![]() 作检核。
作检核。
(4)然后再用前方交会公式(6-38)计算P点坐标。
为判断P点精度,必须在P点对第四个已知点D进行观测,测出![]() 。利用已计算出的P点坐标和A、D两点坐标反算
。利用已计算出的P点坐标和A、D两点坐标反算![]() ,求出
,求出![]() 为:
为:
![]() (6-44)
(6-44)
对于图根点,![]() 容许值为±40″。
容许值为±40″。
表6-11为用余切公式计算后方交会点算例。![]()
后方交会计算表(余切公式) 表6-11
(5)后方交会的危险圆
当待定点P位于三个已知点A、B、C的外接圆时,无论P点位于该圆任何位置,其![]() 和
和![]() 均不变,因此P点无解。故称此外接圆为危险圆。见图6-22,当P点在危险圆上时,则有:
均不变,因此P点无解。故称此外接圆为危险圆。见图6-22,当P点在危险圆上时,则有:
![]() (6-45)
(6-45)
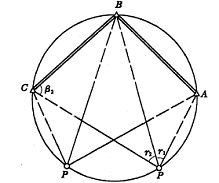
6-22 后方交会的危险圆
将![]() 值代入式(6-41),该式无解。实际工作中,P点位于危险圆上的情况是极偶然的,但是在危险圆附近时,计算出的坐标误差会很大。为了避免P点落在危险圆附近,规定后方交会角
值代入式(6-41),该式无解。实际工作中,P点位于危险圆上的情况是极偶然的,但是在危险圆附近时,计算出的坐标误差会很大。为了避免P点落在危险圆附近,规定后方交会角![]() 、
、![]() 与固定角B不应在160°~180°之间,否则应重新选择点位。
与固定角B不应在160°~180°之间,否则应重新选择点位。
6.5.3 距离交会
随着电磁波测距仪的应用,距离交会也成为加密控制点的一种常用方法。如图6-23,在两个已知点A、B上分别量至待定点![]() 的边长
的边长![]() ,求解
,求解![]() 点坐标,称为距离交会。
点坐标,称为距离交会。
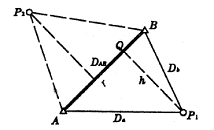
图6-23 距离交会
下面介绍具体定点方法:
(1)根据已知点A、B坐标(![]() )和(
)和(![]() )求方位角
)求方位角![]() 和边长
和边长![]() 。
。
(2) 过![]() 点作AB垂线交于Q点。垂距
点作AB垂线交于Q点。垂距![]() 为
为![]() ,
,![]() 为
为![]() ,利用余弦定理求A角。
,利用余弦定理求A角。
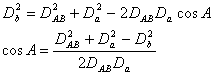 (6-46)
(6-46)
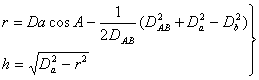 (6-47)
(6-47)
(3) ![]() 点坐标为:
点坐标为:
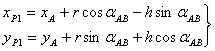 (4-48)
(4-48)
上式P1点在AB线段右侧(A、B、P1顺时针构成三角形)。
若待定点P2在AB线段左侧(A、B、P2逆时针构成三角形),公式为:
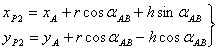 (6-49)
(6-49)
距离交会计算举例见表6-12。
距离交会计算表 表6-12
|
略图与公式 |
|
|
|||||
|
已知坐标 |
|
1035.147 |
|
2601.295 |
观测数据 |
|
703.760 |
|
|
1501.295 |
|
3270.053 |
|
670.486 |
||
|
|
55°07′20″ |
|
815.188 |
|
435.641 |
||
|
|
552.716 |
|
1737.692 |
|
2642.625 |
||
§6.6 三、四等水准测量
三、四等水准测量,除用于国家高程控制网的加密外,还常用作小地区的首级高程控制,以及工程建设地区内工程测量和变形观测的基本控制。三、四等水准网应从附近的国家高一级水准点引测高程。
工程建设地区的三、四等水准点的间距可根据实际需要决定,一般为1~2km左右,应埋设普通水准标石或临时水准点标志,亦可利用埋石的平面控制点作为水准点。在厂区内则注意不要选在地下管线上方,距离厂房或高大建筑物不小于25m,距振动影响区5m以外,距回填土边不少于5m。
三、四等水准测量的要求和施测方法是:
①三、四等水准测量使用的水准尺,通常是双面水准尺。两根标尺黑面的尺底均为0,红面的尺底一根为4.687m,一根为4.787m。
②视线长度和读数误差的限差见表6-13;高差闭合差的规定见表6-4。
三、四等水准测量限差 表6-13
|
等级 |
标准视线长度 (m) |
前后视距差 (m) |
前后视距累计差(m) |
红黑面读数差 (mm) |
红黑面高差之差 (mm) |
|
三 四 |
75 100 |
3.0 5.0 |
5.0 10.0 |
2.0 3.0 |
3.0 5.0 |
三、四等水准测量的观测与计算方法如下:
三(四)等水准测量观测手簿 表6-14
测段:A~B 日期:1993年5月10日 仪器:上光60252
开始:7时05分 天气:晴、微风 观测者:李 明
结束:8时07分 成像:清晰稳定 记录者:肖 钢
|
测站编号 |
点号 |
后尺 |
下 丝 |
前尺 |
下丝 |
方向及 尺 号 |
中丝水准尺读数 |
K+黑-红 |
平均 高差 |
备注 |
|
|
上丝 |
上丝 |
黑色面 |
红色面 |
||||||||
|
|
|
(1) (2) (9) (11) |
(4) (5) (10) (12) |
后 前 后-前 |
(3) (6) (15) |
(8) (7) (16) |
(14) (13) (17) |
(18) |
|
||
|
1 |
A~转1 |
1.587 1.213 37.4 -0.2 |
0.755 0.379 37.6 -0.2 |
后 前 后-前 |
1.400 0.567 +0.833 |
6.187 5.255 +0.932 |
0 -1 +1 |
+0.8325 |
|
||
|
2 |
转1~转2 |
2.111 1.737 37.4 -0.1 |
2.186 1.811 37.5 -0.3 |
后02 前02 后-前 |
1.924 1.998 -0.074 |
6.611 6.786 -0.175 |
0 -1 +1 |
-0.0745 |
|
||
|
3 |
转2~转3 |
1.916 1.541 37.5 -0.2 |
2.057 1.680 37.7 -0.5 |
后01 前02 后-前 |
1.728 1.868 -0.140 |
6.515 6.556 -0.041 |
0 -1 +1 |
-0.1405 |
|
||
|
4 |
转3~转4 |
1.945 1.680 26.5 -0.2 |
2.121 1.854 26.7 -0.7 |
后02 前01 后-前 |
1.812 1.987 -0.175 |
6.499 6.773 -0.274 |
0 +1 -1 |
-0.1745 |
|
||
|
5 |
转4~B |
0.675 0.237 43.8 +0.2 |
2.902 2.466 43.6 -0.5 |
后01 前02 后-前 |
0.466 2.684 -2.218 |
5.254 7.371 -2.117 |
-1 0 -1 |
-2.2175 |
|
||
(1)一个测站上的观测顺序(参见表6-14)
照准后视尺黑面,读取下、上、中丝读数(1)、(2)、(3);
照准前视尺黑面,读取下、上丝读数(4)、(5)及中丝读数(6);
照准前视尺红面,读取中丝读数(7);
照准后视尺红面,读取中丝读数(8)。
这种“后—前—前—后”的观测顺序,主要是为抵消水准仪与水准尺下沉产生的误差。四等水准测量每站的观测顺序也可以为“后—后—前—前”,即“黑—红—黑—红”。
表中各次中丝读数(3)、(6)、(7)、(8)是用来计算高差的。因此,在每次读取中丝读数前,都要注意使符合气泡的两个半像严密重合。
(2)测站的计算、检核与限差
①视距计算
后视距离:(9)=(1)-(2)。
前视距离:(10)=(4) -(5)。
前、后视距差:(11)=(9) -(10)。三等水准测量,不得超过土3m,四等水准测量,不得超过±5m。
前、后视距累积差:本站(12)=前站(12)+本站(11)。三等水准测量不得超过±5m,四等水准测量不得超过±10m。
②同一水准尺黑、红面读数差
前尺:(13)=(6)+![]() -(7)。
-(7)。
后尺:(14)=(3)+ ![]() -(18)。
-(18)。
三等水准测量不得超过±2mm,四等水准测量不得超过±3mm。K1、K2分别为前、后尺的红、黑面常数差。
③高差计算
黑面高差:(15)=(3)-(6)
红面高差:(16)=(8)-(7)
检核计算:(17)=(14)-(13)=(15)-(16) ±0.100。三等水准测量不得超过3mm,四等水准测量不得超过5mm。
高差中数:(18)=![]() {(15)+[(16)
±0.100]}。
{(15)+[(16)
±0.100]}。
上述各项记录、计算见表6-14。观测时,若发现本测站某项限差超限,应立即重测,只有各项限差均检查无误后,方可移站。
(3)每页计算的总检核
校核计算:
在每测站检核的基础上,应进行每页计算的检核。

测站数为偶数时:
![]()
测站数为奇数时:
![]()
(4) 水准路线测量成果的计算、检核
三、四等附合或闭合水准路线高差闭合差的计算、调整方法与普通水准测量相同(见第2章)。
当测区范围较大时,要布设多条水准路线。为了使各水准点高程精度均匀,必须把各线段连在一起,构成统一的水准网,采用最小二乘法原理进行平差,从而求解出各水准点的高程。
§6.7 三角高程
当地面两点间地形起伏较大而不便于水准施测时,可应用三角高程测量的方法测定两点间的高差而求得高程。该法较水准测量精度低,常用于山区各种比例尺测图的高程控制。
6.7.1 三角高程测量原理
三角高程测量是根据测站与待测点两点间的水平距离和测站向目标点所观测的竖直角来计算两点间的高差。
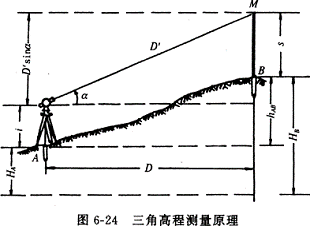
如图6-24,已知A点高程![]() ,欲求B点高程
,欲求B点高程![]() 。将仪器安置在A点,照准B目标顶端M,测得竖直角
。将仪器安置在A点,照准B目标顶端M,测得竖直角![]() 。量取仪器高
。量取仪器高![]() 和目标高
和目标高![]() 。如果测得AM之间距离D′,则高差
。如果测得AM之间距离D′,则高差![]() 为:
为:
![]() (6-50)
(6-50)
如果两点间平距为D,则A、B高差为:
![]() (6-51)
(6-51)
B点高程为:
![]()
6.7.2 地球曲率和大气折光对高差的影响
上述是在假定地球表面为水平面(即把水准面当作水平面),认为观测视线是直线的条件下导出的。当地面上两点间的距离小于300m时是适用的。两点间距离大于300m时就要顾及地球曲率,加以曲率改正,称为球差改正。同时,观测视线受大气垂直折光的影响而成为一条向上凸起的弧线,必须加以大气垂直折光差改正,称为气差改正。以上两项合称为球气差改正,简称二差改正。
如图6—25,O为地球中心,R为地球曲率半径(R=6371km),A、B为地面上两点,D为A、B两点间的水平距离,R′为过仪器高P点的水准面曲率半径,PE和AF分别为过P点和A点的水准面。实际观测竖直角![]() 时,水平线交于G点,GE就是由于地球曲率而产生的高程误差,即球差,用符号c表示。由于大气折光的影响,来自目标N的光沿弧线PN进人仪器望远镜,而望远镜却位于弧线PN的切线PM上,MN即为大气垂直折光带来的高程误差,即气差,用符号
时,水平线交于G点,GE就是由于地球曲率而产生的高程误差,即球差,用符号c表示。由于大气折光的影响,来自目标N的光沿弧线PN进人仪器望远镜,而望远镜却位于弧线PN的切线PM上,MN即为大气垂直折光带来的高程误差,即气差,用符号![]() 表示。
表示。
图6-25 三角高程及二差影响
由于A、B两点间的水平距离D与曲率半径R′之比值很小,例如当D=3km时,其所对圆心角约为2′.8,故可认为PG近似垂直于OM,则
![]()
于是,A、B两点高差为:
![]() (6-52)
(6-52)
令![]() ,则公式为:
,则公式为:
![]() (6-53)
(6-53)
从图6-25可知,
![]()
即
![]()
![]() 与
与![]() 相比很小,可略去,并考虑到
相比很小,可略去,并考虑到![]() 与
与![]() 相差甚小,故以
相差甚小,故以![]() 代替
代替![]() ,则上式为:
,则上式为:
![]() (6-54)
(6-54)
根据研究,因大气垂直折光而产生的视线变曲的曲率半径约为地球曲率半径的7倍,则
![]() (6-55)
(6-55)
二差改正为:
![]() (6-56)
(6-56)
水平距离D以公里为单位。
表6-15给出了1km内不同距离的二差改正数。
二差改正数表 表6-15
|
D(km) |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
0.9 |
1.0 |
|
|
0 |
0 |
1 |
1 |
2 |
2 |
3 |
4 |
6 |
7 |
三角高程测量一般都采用对向观测,即由A点观测B点,再由B点观测A点,取对向观测所得高差绝对值的平均数可抵消两差的影响。
6.7.3 三角高程测量的观测和计算
(1)三角高程测量的观测
①安置经纬仪于测站上,量取仪器高![]() 和目标
和目标![]() 。
。
②当中丝瞄准目标时,将竖盘水准管气泡居中,读取竖盘读数。必须以盘左、盘右进行观测。
③竖直角观测测回数与限差应符合表6-16的规定。
④用电磁波测距仪测量两点间的倾斜距离D′,或用三角测量方法计算得两点间的水平距离D。
竖直角观测测回数及限差见表6-16
 竖直角观测测回数及限差表
表6-16
竖直角观测测回数及限差表
表6-16
|
|
四等和一、二级小三角 |
一、二、三级导线 |
||
|
DJ2 |
DJ6 |
DJ2 |
DJ6 |
|
|
测回数 |
2 |
4 |
1 |
2 |
|
各测回竖直角互差限差 |
15〝 |
25〝 |
15〝 |
25〝 |
(2)三角高程测量计算
三角高程测量往返测所得的高差之差(经两差改正后)不应大于0.1Dm(D为边长,以公里为单位)。
三角高程测量路线应组成闭合附合路线。如图6-26,三角高程测量可沿A-B-C-D-A闭合路线进行,每边均取对向观测。观测结果列于图上,其路线高差闭合差![]() 的容许值按下式计算:
的容许值按下式计算:
![]() (6-57)
(6-57)
式中D以公里为单位
若![]() ,则将闭合差按与边长成正比分配给各高差,再按调整后的高差推算各点的高程。图6-26计算见表6-17。
,则将闭合差按与边长成正比分配给各高差,再按调整后的高差推算各点的高程。图6-26计算见表6-17。
图6-26 三角高程测量观测成果略图
三角高程测量的高差计算表 表6-17
|
起算点 |
A |
B |
… |
||
|
欲求点 |
B |
C |
… |
||
|
|
往 |
返 |
往 |
返 |
|
|
水平距离D(m) |
581.38 |
581.38 |
488.01 |
488.01 |
… |
|
竖直角 |
+11°38′30″ |
-11°24′00″ |
+6°52′15″ |
-6°34′30″ |
… |
|
仪器高 |
1.44 |
1.49 |
1.49 |
1.50 |
… |
|
目标高 |
-2.50 |
-3.00 |
-3.00 |
-2.50 |
… |
|
两差改正 |
+0.02 |
+0.02 |
+0.02 |
+0.02 |
… |
|
高差(m) |
+118.74 |
-118.72 |
+57.31 |
-57.23 |
… |
|
平均高差(m) |
+118.73 |
+57.27 |
… |
||