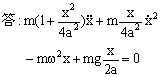当前位置：学习内容 –习题

7.1 质量为m的质点，在重力场中以初速u₀和水平线成a角抛射。用哈密顿原理求该质点的运动微分方程和运动积分。(解答)

答：运动微分方程为，

运动积分为

图7.2	图7.5	图7.8

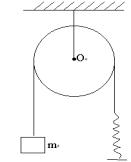
7.2 如图所示，一滑轮可绕通过轮心的水平轮转动。在此滑轮上绕过一条不可伸

长的绳，绳的一端悬一砝码，其质量为m，另一端则固结在一竖直弹簧上，弹簧下端连地，设弹簧中张力与伸长成正比，比例常数为k。滑轮的质量已知为M，并分布在轮缘上。试用哈密顿原理求砝码的振动周期。假定绳与滑轮之间无滑动。(解答)

答：

7.3 试用哈密顿原理求复摆作微振动时的周期。(解答)

答：

式中m是复摆的质量，I₀是复摆绕悬点振动时的转动惯量。l为复摆重心G与悬点O之间的距离，g为重力加速度。

7.4 依哈密顿原理，推导哈密顿正则方程。(解答)

7.5 设质量为m的质点受重力作用，被约束在半顶角为a的圆锥面内运动。试以r、q为广义坐标，用哈密顿原理求质点的运动微分方程。(解答)

答：

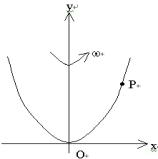
7.6 试用哈密顿正则方程求单摆的运动方程。(解答)

答：

7.7 轴为竖直而顶点在下的抛物线形金属丝，以匀角速w绕轴转动。一质量为m的小环套在此金属丝上，并可绕金属丝滑动。试用正则方程求小球在x方向的运动微分方程。已知抛物线的方程为x²=4ay，式中a为常数。(解答)

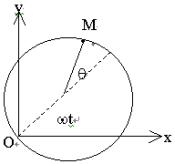
7.8 小环M，套在光滑圆圈上，并可沿着圆圈滑动。如圆圈在水平面内以匀角速w绕圈上某点O转动，试用正则方程求小环沿圆圈切线方向的运动微分方程。(解答)

答：

7.9 试求由质点系的动量p和角动量J的笛卡儿分量所组成的泊松括号。(解答)

答：[J_x，p_x] = 0，[J_x，p_y] = p_z，[J_x，p_z] = -p_y。

7.10 试证

(解答)

。

7.11 试利用正则变换，由正则方程求竖直上抛物体的运动规律。已知本问题的母函数，式中q为确定物体位置的广

义坐标，Q为变换后新的广义坐标，g为重力加速度。(解答)

7.12 一自由质点的质量为m，处于保守场中，试确定其哈密顿—雅可比方程(分别用笛卡儿坐标和圆柱坐标)。(解答)

答：笛卡儿坐标系中

柱坐标系中