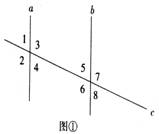
教学过程：

1．

创设情景

（1）电脑显示一个房屋的屋顶、楼梯、门等现实生活中的物体、并请学生找出其中蕴藏着的平行线；

（2）从同学们的答案中抽象出图①

（3）请学生找出同位角、内错角、同旁内角（电脑显示结论）。

从学生熟悉的事物导入，即使学生复习了旧课，又培加了学生学习的兴趣。

2．探索1：

（1）提出问题 

请你用可能的方法在图①中找出所有角之间的数量关系

（2）活动；

以小组为单位展开讨论，比较这8个角的数量关系，并鼓励学生大胆使用科学而有效的方法。

这里学生可以使用量角器量出度数进行比较，也可以用纸将每个角按实际大小剪下来比较等方法。总之，尽可能地鼓励学生寻找有效的方法）

3）演示探索1：

请各小组的代表演示各组的讨论方法：

教师小结：注意启发学生可将这些关系分为哪几类（电脑演示）。

相等关系：

∠1=∠4；∠5=∠8；∠2=∠3；∠6=∠7；

∠1=∠5；∠3=∠7；∠2=∠6；∠4=∠8；

∠1=∠4=∠5=∠8

∠3=∠6=∠7=∠2

互补关系

∠1+∠2=180°；∠3+∠4=180°；∠5+∠6=180°； 

∠7+∠8=180°；∠3+∠5=180°；∠4+∠6=180°

以开放性问题的形式提出问题，创设了宽松的教学环境，有利于学生积极思考，主动参与，培养了学生的发散思维能力。

3．探索2：

（1）提出问题：

在这些关系中，哪些与直线a和b都有关？哪些只与直线a有关，哪些只与直线b有关？

（2）活动：

将学生平分为三个大组，一组找与直线a和b都有关的式子；一组找只与直线a有关的式子；另一组找只与直线b有关的式子。

请各组代表公布结论。

教师小结（电脑显示）。

让学生有创新地开展数学活动，培养了学生动手和探索问题的能力。

①与直线a和b都有关的式子有：

相等：

∠1=∠5；∠3=∠7；∠2=∠6； 

∠4=∠8；∠3=∠6；∠4=∠5；

∠1=∠8；∠2=∠7

互补：

∠3+∠5=180°；∠4+∠6=180°；

∠1+∠7=180°；∠2+∠8=180°；

②只与直线a有关的式子；

相等：

∠1=∠4；∠2=∠3

互补：

∠1+∠2=180°；∠3+∠4=180°

③只与直线b有关的式子。

相等：

∠5=∠8；∠6=∠7

互补：                

∠5+∠6=180°；∠7+∠8=180° ；

渗透分类思想

4．探索3：

（1）提出问题：

从上面的讨论可知，只与直线a 或b有关的式子是无需从a∥b的关系中推出的，也即它们的成立与否不以a∥b为前提。那么与a 和b有关的式子，若改变a与b的位置关系，它们还成立吗？

（2）活动：

以小组为单位探索a与b不平行的情况（主要是电脑列出图的几个角），启发学生得出结论：当a 和b不平行时，电脑所列图①中的式子不再成立，进而可知，这些关系式是以a∥b为基础的，是a∥b时特有的式子。

教师的点拨使学生找到探索的方法，并将问题的开放性进行适当调控，使问题向着预定目标进行。

5．探索4：

（1）提出问题；

具有相等关系的角具有怎样的位置关系；

具有互补关系的角具有怎样的位置关系；

（2）分组讨论，提出结论；

具有相等关系的角有：同位角、内错角和一些没学过的位置关系角。

具有互补关系的角有：同旁内角和一些没学过的位置关系角。

排除非本质特征进行本质特征归纳，从而得出本节课的中心内容。

6．探索5：                       

（1）提出问题；

如果不考虑那些没学过的角的位置关系，只对同位角、内错角、同旁内角进行归纳总结……如果两条平行线被第三条直线所截，则……

（2）请学生回答，从而得出本节课的结论。

7．点题（电脑显示）：

（1）平行线的性质定理；

（2）对比平行线的判定定理；

（3）共同讨论它们的异同。

8． 问题解决：

问题：小明的妈妈在装修房子时要把画挂在墙上，可是几次都挂歪了。老师想请一个同学帮帮她，并请你在黑板上演示一下。请同学们分组讨论后派一名代表来完成任务。

通过问题解决使学生体验数学与现实生活的联系，激起学生学习数学的兴趣。

点评：本节课通过开放式的教学模式，打破常规，请学生通过动手、动脑和协作学习来探索问题，得出猜想，即培养了学生的猜想能力，又使学生经历了从特殊到一般和从实践到理论的过程。另外，步步深入的教学方式使学生的探索活动始终围绕本节课的主题展开。