习题4

 

习题4.1  证明

                    

习题4.2  已知算符 满足对易关系 ， 是 的可微函数，证明

                    

                    

                    

                    

习题4.3  证明

                    

进而证明

                        

习题4.4  定义算符

                       

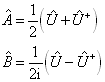
式中，算符 是幺正算符。证明 与 皆为厄米算符，并且满足

                        

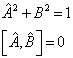
习题4.5  设哈密顿算符 的本征解为 和 ，对任意的线性厄米算符 ，证明下式成立

                  

   习题4.6  设粒子处于宽度为 的对称一维无限深势阱中，若 时粒子的状态为

       

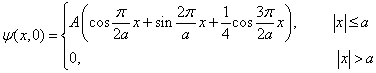
求 时刻的波函数。

习题4.7  质量为 的粒子在宽度为 的非对称一维无限深势阱中运动，若 粒子处于已经归一化的状态

                    

求， 时能量 的取值几率； 时的波函数和能量取值几率分布。

习题4.8  质量为 的粒子在宽度为 的非对称二维无限深势阱

                

                 

中运动，若 时粒子处于状态

    

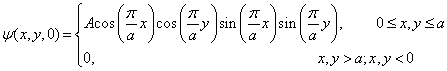
问，下面各组力学量 是否构成力学量完全集。分别求出 和 时能量的取值几率与平均值。

习题4.9  证明在 的本征态下， 。进而证明角动量沿与 轴成 角的方向上的分量的平均值为 。

习题4.10   时，平面转子处于状态

                      

求 时 的可能取值与相应的取值几率。

习题4.11  证明