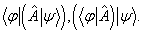§5 深入研究、学习的内容:关于狄拉克符号内积的讨论
1.
由(5。3。1)式可看出,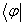 与
与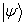 是对称的。
是对称的。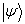 被称为右矢,则
被称为右矢,则
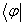 应称为左矢,并且这样的左矢也形成了一个矢量空间。这里要澄清一个概念,不要把(5。3。1)式理解为“定义一个左矢
应称为左矢,并且这样的左矢也形成了一个矢量空间。这里要澄清一个概念,不要把(5。3。1)式理解为“定义一个左矢 和一个右矢
和一个右矢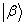 的内积为
的内积为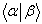 ,它是一个复数,并且
,它是一个复数,并且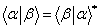 。”。这是错误的,因为只有对同一个矢量空间的矢量才能有内积的定义。内积的定义是,
。”。这是错误的,因为只有对同一个矢量空间的矢量才能有内积的定义。内积的定义是,
设L是一个复线性空间,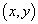 :
: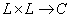 是一个从笛卡尔乘积集合
是一个从笛卡尔乘积集合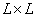 到复数集合的映射,且有下列性质:
到复数集合的映射,且有下列性质:
(1) 对一切
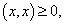 当且仅当
当且仅当
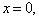
(2) 对一切 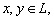 有
有
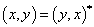 ;
;
(3) 对一切  有
有
(4) 对一切 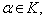 一切
一切 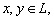 有
有
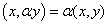 ,
,
则称此映射为L上的一个内积.
这里矢量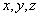 都属于同一个矢量空间
都属于同一个矢量空间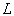 。
。 显然不属于右矢空间,所以对左矢空间的一个矢量
显然不属于右矢空间,所以对左矢空间的一个矢量 和右矢空间的一个矢量
和右矢空间的一个矢量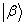 定义内积是错误的。
定义内积是错误的。
那么应怎样正确地理解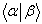 这个记号呢?
这个记号呢?
一个简捷的解释是如前所述,把态矢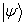 和
和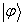 的内积记为,或把
的内积记为,或把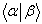 就看作为两个态函数
就看作为两个态函数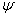 和
和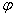 (它们自然属于同一个矢量空间)的内积,即,
(它们自然属于同一个矢量空间)的内积,即,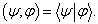 。这个解释的不足之处是只承认存在右矢空间,没有左矢空间或没有直接回答左矢及左矢空间是什么。
。这个解释的不足之处是只承认存在右矢空间,没有左矢空间或没有直接回答左矢及左矢空间是什么。
当把 看作左矢时,对
看作左矢时,对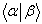 的确切理解如下:
的确切理解如下:
首先定义在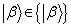 上的线性泛函
上的线性泛函 。线性泛函
。线性泛函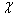 是一种线性运算,它将每一个右矢
是一种线性运算,它将每一个右矢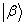 和一个复数联系起来:
和一个复数联系起来:
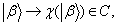
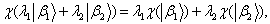
能够证明,定义在右矢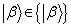 上的线性泛函的集合
上的线性泛函的集合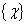 形成了一个矢量空间,称为
形成了一个矢量空间,称为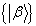 的对偶空间,记为
的对偶空间,记为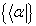 。
。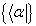 中的每一个元素,或矢量,都叫作左矢,记为
中的每一个元素,或矢量,都叫作左矢,记为 。线性泛函
。线性泛函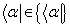 作用于右矢
作用于右矢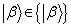 得到的那个数记作
得到的那个数记作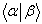 ,亦即,
,亦即,
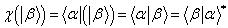 ,
,
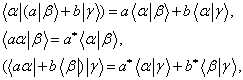
式中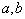 是任意复数。由上式可见,
是任意复数。由上式可见,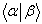 对于右矢是线性的,对于左矢是反线性的。
对于右矢是线性的,对于左矢是反线性的。
在微分几何中,对偶空间是通过一次形式来定义的。一次形式定义为矢量的线性(复或实)函数。其意义如下:P点的一个一次形式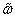 ,使得P点的一个矢量
,使得P点的一个矢量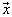 对应一个复数,
这个数记作
对应一个复数,
这个数记作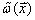 。这个矢量上的函数
。这个矢量上的函数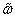 满足
满足
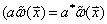
容易看出,点P处的所有一次形式满足矢量空间的公理。这个矢量空间称为对偶空间。容易看出矢量和相应的一次形式是互为对偶的。有以下几种表达方式:
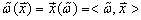 。
。
由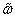 作用于
作用于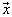 得到的这个数
得到的这个数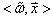 叫作
叫作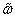 和
和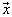 的缩并。在较早的文献中,矢量常常被称为逆变矢量,而一次形式被称为协变矢量。
的缩并。在较早的文献中,矢量常常被称为逆变矢量,而一次形式被称为协变矢量。
在这里,右矢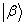 就是矢量,左矢
就是矢量,左矢 就是它的一次形式,反之亦然。
就是它的一次形式,反之亦然。
综上所述可见,‘定义一个左矢 和一个右矢
和一个右矢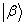 的内积为
的内积为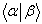 ’是不正确的。正确的表述应该是“
’是不正确的。正确的表述应该是“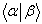 是左矢
是左矢 (右矢的一次形式)作用于右矢得到的一个数,称为左矢
(右矢的一次形式)作用于右矢得到的一个数,称为左矢 和右矢
和右矢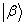 的缩并
的缩并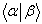 ”。
”。
2.涉及反线性算符时应用狄拉克符号的注意点
具有下列性质的算符称为反线性算符
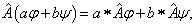
这里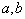 是任意复数。其与线性算符
是任意复数。其与线性算符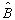 的本质差别在于,
的本质差别在于,
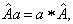 而
而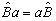 。
。
相应地,反线性算符的厄米共轭算符的定义也要改变
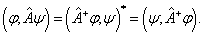
反线性算符的么正算符,即反么正算符的定义是
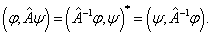
比较上式可得
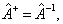
这与么正算符与厄米共轭算符的关系相同。反线性算符在讨论时间反演时是必须的。
对于线性算符,有
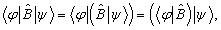
因为
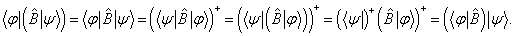
对于反线性算符,
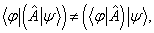
因为
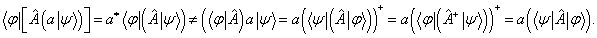
可见,对于反线性算符,要明确地区分