习题8
习题8.1
设哈密顿算符的矩阵形式为
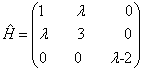
求其精确的本征值；若 
，用微扰论求其本征值到二级近似。
习题8.2
当 
为一小量时，求矩阵
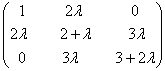
的本征值至 的二次项，本征矢至
的一次项。
习题8.3 证明无简并微扰论的如下公式
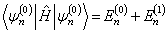
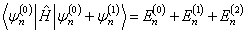
习题8.4
在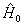 
表象中，若哈密顿算符的矩阵形式为
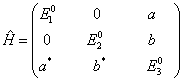
其中，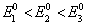 
。利用微扰论求能量至二级近似。
习题8.5 线谐振子受到微扰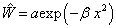 
的作用，计算基态能量的一级修正。其中，常数 
。
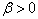习题8.6 一个电荷为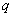 
的线谐振子受到恒定弱电场 
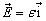的作用，利用微扰论求其能量至二级近似，并与其精确结果比较。
习题8.7 线谐振子受到微扰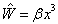 
的作用，求其能量的二级修正、基态与第一激发态波函数的一级修正。
习题8.8 粒子在一维势阱
中运动，求其能量的一级修正。其中，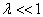 
。
习题8.9 转动惯量为 
、电矩为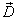 
的空间转子处于均匀弱电场 
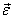中，用微扰论求基态能量到二级修正。
习题8.10 若类氢离子的核不是点电荷，而是半径为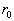 
及电荷均匀分布的小球，试计算这种效应对类氢离子基态能量的一级修正。提示：此时类氢离子的位势为
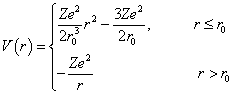
习题8.11
在 
表象中，体系的哈密顿算符为
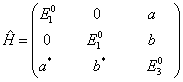
其中，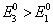 
。用简并微扰论求能量至二级近似，并与严格解比较。
习题8.12
自旋为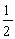 
的粒子处于一维无限深势阱（ 
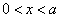）中，若其受到微扰
的作用，求基态能量至二级修正。其中，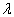 
为一小量。
习题 8.13 用试探波函数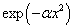 
计算线谐振子的基态能量与波函数。
习题8.14 以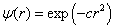 
为试探波函数，求氢原子基态能量与波函数。其中， 
。
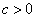习题8.15
设电子处于势场
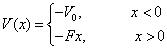
中，当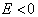 
时，求其透射系数。此即在强电场作用下，电子隧穿金属表面的简化模型。
习题8.16
把氢原子置于如下电场中
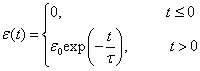
当时间足够长时，求氢原子从基态跃迁到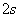 
及 
态的几率。
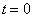时，电荷为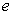 
的线谐振子处于基态，若在 
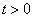时加一与振动方向相同的恒定外电场 
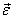，求其处于任意态的几率。