习题1
习题1.1 由黑体辐射公式导出维恩位移定律,即
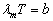 ,并计算出常数
,并计算出常数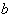 的近似值。
的近似值。
习题1.2 利用玻尔-索末菲量子化条件求限制在方形箱内运动粒子的能量,箱的长、宽和高分别为 、
、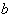 和
和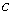 。
。
习题1.3 利用玻尔-索末菲量子化条件求转动惯量为 的平面转子的能量。
的平面转子的能量。
习题1.4 计算如下粒子的德布洛意波长
(1) 动能为 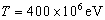 的
的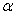 粒子
,
粒子
,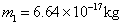 ;
;
(2) 速度 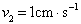 、质量
、质量
 的尘埃;
的尘埃;
(3) 速度 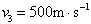 、质量
、质量
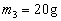 的子弹。
的子弹。
习题1.5 有一功率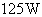 的水银灯,其发光效率为80%,若只有2%的能量用于发射光子,求每秒发射波长为
的水银灯,其发光效率为80%,若只有2%的能量用于发射光子,求每秒发射波长为
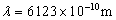 的光子数。
的光子数。
习题1.6 若电子与中子的德布洛意波长均为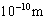 ,求它们各自具有的能量。若它们的速度相等,求出电子与中子波长之比的值。
,求它们各自具有的能量。若它们的速度相等,求出电子与中子波长之比的值。
习题1.7为了观察微粒的布朗(Bulang)运动,在液体中放入直径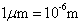 、质量为
、质量为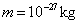 的悬浮微粒,在常温
的悬浮微粒,在常温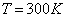 下,其热运动的动能为
下,其热运动的动能为
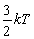 ,求该微粒的德布洛意波长,并说明有无必要将其视为量子客体。
,求该微粒的德布洛意波长,并说明有无必要将其视为量子客体。
习题1.8 由

及
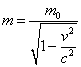
出发,利用

导出相对论粒子的德布洛意波长与动能的关系。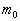 为该粒子的静止质量。
为该粒子的静止质量。
习题1.9 哪个实验证明了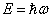 ,哪个实验证明了
,哪个实验证明了
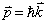 ?
?
;