第二节 标准分数指出学生在团体中的相对地位、解释测验分数在组内相对水平的另一种方法，是确定测验成绩的标准分数。
标准分数是以标准差为单位表示测验成绩与平均分数之间的距离。
假定某常模团体含有N个被试,他们在某一测验上的测验分数可记为
；再设
和S分别表示常模团体在该测验上的平均分数和标准差；那么，分数列
中任一个原始分数
所对应的标准分数用符号
表示，其计算公式如下：
（3-1）
或一般地写成
Z =
(3-2)
(这里
=
S=
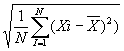
从上面标准分数Z的定义公式可知，标准分数Z是一种以平均数为参照，以测验分数的标准差来衡量原分数在其常模团体中地位高低的一种评定方法。当原分数比平均数来得高时,其相应的标准分数Z为正值；当原分数比平均数来得低时，其相应的标准分数Z将为负数。因此,标准分数Z值可正可负，且一般取值在-3～+3之间。
[例1] 甲、乙、丙、丁四人在某次语文考试中分别获得 72分、68分、 48分和90分，而全体学生的语文平均成绩为60分,标准差为12分，则这4个相应的标准分数分别为：
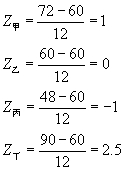
[例2] 对某校高二学生进行期中学习质量检测,语文、数学和英语成绩的平均数分别是80分、70分和85分，这三种成绩的标准差分别是10分、15分和12分。某学生的三科成绩分别是85分、82分和90分,问：该生这三科成绩哪一科最好？
为回答这一问题，必须用标准分数来比较。根据公式3-2,不难得到：
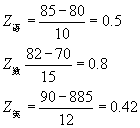
可见，
，故可认为该生的数学成绩相对最好，其次为语文，再次是英语。
在标准分数Z的应用中，由于标准分数Z分值过小，并往往带有小数和负值等缺陷，在许多情形下直接使用不大合乎人们表示分数的习惯，故通常把标准分数Z通过线性变换，转到更大的标准分数量表上，其一般转换公式为：T=a+bZ （２-3）
上式中，a和b为选定的两个常数，Z为标准分数，T为线性变换的标准分数。常见的有如下几种：
①教育与心理测验中的T分数：T=50+10Z
②韦氏智力量表中各分测验的量表分：T=10+3Z
韦氏智力量表智商（离差智商）：IQ=100+15Z
③美国大学入学考试报告分数：CEEB=500+100Z
④为出国人员举行的英语水平考试：EPT=90+20Z
⑤美国教育测验中心举办“托福”考试：TOEFL=500+70Z
所谓标准分数常模，就是以常模团体在某一测验上的实测数据为基础，把原始分数转换成基本标准分数Z或转换到更大的标准分数T量表上，能够揭示每个测验分数在常模团体测验分数中的相对地位的一种组内常模。不难明白，建立标准分数常模实际上就是根据常模团体的实测数据， 利用公式（3-1）或（3-3），在原始分数序列
之间或者与标准分数
之间,建立起对应关系，从而形成某种测验的标准分数常模。若用规范的表来表达标准分数常模，即形成标准分数常模转换表。这类常模转换表有两种类型，一种是简单式常模转换表，它一般是将单个测验的原始分数转换成标准分数量表分；如表3-2所示。另一种是复合式常模转换表,它一般是把成套测验的若干个分测验安排在同一个常模表上转换成标准分数量表分，如表3-3所示。
表3-2 简单式常模表示例
原始分
量表分（T=50+10Z）
100
90
80
70
60
50
69
66
63
60
57
54
表3-3复合式常模表示例
量表分
常识
词汇
算术
类同
理解
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
0-3
4-5
6-7
8
9
10
11
12
13
14
—
15
16
17
18
—
19
20
21-23
0-3
3
4-5
6
7-8
9-10
11-12
13-14
15-16
17
18-19
20-24
25-26
27
28-29
30
31-32
33-35
36-44
0-3
4-5
6-8
9
10
11
12
13
14
15
16
—
17
18
—
19
—
20
—
0-1
2-3
4
5-6
7
8-9
10
11
12
13
14-15
16
17
18
19
20
—
21
22
0-2
3-6
7-8
9
10
11
12-13
14-15
16
17
18
19
20
21
22
23
24-25
26
27-30
资料取自：韦氏学前儿童智力量表的上海市常模。
（一）标准分数Z的性质与特点
标准分数Z具有如下一些性质与特点：
（1）任何一批原始分数，转化成Z分数后，这批Z分数的平均值为0，标准差为1。
（2）在一般情况下，标准分数Z的取值范围在-3到+3之间。
（3）标准分数Z量表的单位是相等的，其零点是相对的。因此，不同科目的Z分数具有较好的可比性和可加性。
（4）Z分数本身是关于原始分数X的一种线性变换，因此，不同科目的Z分数具有较好的可比性和可加性。
（5）Z分的意义可以用正态分布曲线下的面积比例（本质上是概率值）做出最好的解释。
（二）正态分布下标准分数Z和百分数等级PR之间的关系
标准分数Z是与百分等级PR相联系的一种相对分数,在正态分布下,其对应的百分等级PR与一个以标准分数Z为界点的正态曲线左尾部面积比例相对应。 这种对应关系由统计学家编制出正态分布面积表供人的查表确定。通过查正态分布表（见附表1），只要简单计算，就可以确定某个Z分数所对应的百分等级。 例如， 当Z=-1时， 计算得到
；当Z=0时，得到
；当Z=1时，
等等。
有关正态分布的内容，我们将在第十章中进一步学习和理解。（三）正态分布下若干评分体系之间的关系
1.标准九分及其与百分等级和标准分数之间的关系
标准九分（Stanine）是基于百分等级形成的另一较常用的评分量表，该评分量表是9点评分形式，取值为1～9的整数。在正态分布下，标准九分量表与标准数Z及百分等级PR之间的关系如表3-4所示。
2.其它多点评分量表
除了上述标准九分量表外，还有标准十分、标准十五分和标准二十分量表等，它们在本质上都是基于百分等级的多点（等级）评分量数。例如卡特尔16PF测验就是采用标准十分量表常模。对于标准十分量表，它在正态分布下，各个分值与百分等级之间的对应关系及各个分值所对应的个案百分比如表所示。3-5。
表3-4 标准九分与其它评分制相互关系
标准九分
Z分范围
百分等级范围
标准九分个案百分比(％)
9
8
7
6
5
4
3
2
1
+1.75以上
+1.25-+1.75
+0.75-+1.25
+0.25-+0.75
-0.25-+0.25
-0.75-+0.25
-1.25-—0.75
-1.75-—1.25
-1.75以下
96-100
89～95
77-88
60-76
41-59
24-40
12-23
5-11
1-4
4
7
12
17
20
17
12
7
4
表 3-5 标准十分与百分等级范围对应表
标准十分
10
9
8
7
6
5
4
3
2
1
百分等级范围
99-100
94- 98
85- 93
70- 84
51- 69
32- 50
17- 31
8- 16
3-7
1-2
所占个案百分比％
2
5
9
15
19
19
15
9
5
2
(四)在一定条件下使用标准分数
标准分数计算方便且具有相当程度的优越性与合理性，在教育测量与评价中有其独特的作用。但是，标准分数使用是基于常模数据服从正态分布的假设。数据只有在正态分布条件下才能使用标准分数计算，这样才能充分体现标准分数的优越性与内涵（ 标准分数Z与百分等级
之间存在着一定的关系）。在实际测试过程中,很可能碰到常模团体的测验分数严重偏态，这种情况下若要直接使用上述的标准分数体系来建立常模就不大妥当。 一种 可行的办法是先对测验分数分布进行正态化（Normalized）处理，而后再建立标准分数常模。其主要步骤如下:
（1）根据常模团体的测验分数次数分布表,建立起原分数{Xi}与百分等级PRi之间的一一对应关系。
（2）利用正态分布面积表（见附表1），从已知的每一个百分等级PRi 反查其对应的标准分数Zi,从而间接实现了从{Xi}到{Zi}之间的变换。
（3）根据需要选择上述公式（3-3）中的a与b两个常数，通过公式（3-3）再次实现
值得注意的是，对于由多个分测验构成的成套测验，若要建立常模，或者利用多个教育测验分数相加的总分进行教育决策，我们要考虑到不同分测验的标准分数是否可加的问题。从理论上讲，只要常模团体在各个分测验上的分数分布形态都接近或相同，那么，利用标准分数建立各个测验的量表分是可行的。且是可加的。而在分数分布形态下一致的情况下，则必须采用正态化处理，即利用正态分布表，从已知的百分等级
