第四节 梁的整体稳定
基本假定:双轴对称工字型截面简支梁纯弯,夹支座(只能绕x轴,y轴转动,不能绕z轴转动,只能自由挠曲,不能扭转)。梁变形后,力偶矩与原来的方向平行。如图:
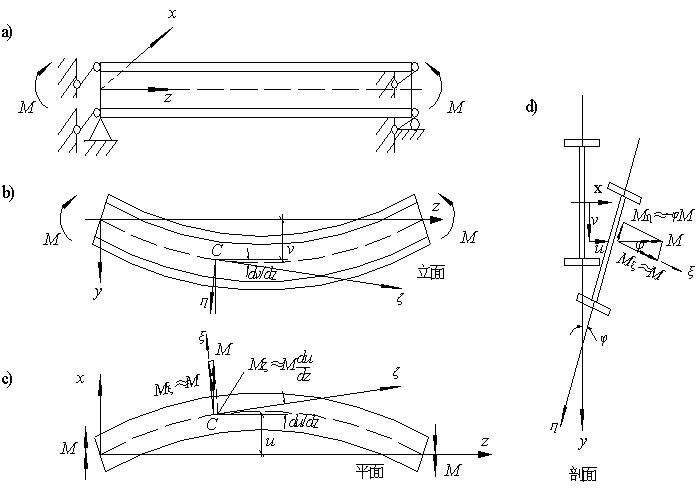
一.梁失稳的现象:侧向弯曲,伴随扭转——出平面弯扭屈曲。
二.原因:受压翼缘应力达临应力,其弱轴为x轴,但由于有腹板作连续支承,(下翼缘和腹板下部均受拉,可以提供稳定的支承),只有向强轴(y轴)方向屈曲,侧向屈曲后,弯矩平面不再和截面的剪切中心重合,必然产生扭转。
三.临界弯矩:
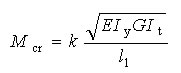
四.影响因素:
1.荷载种类
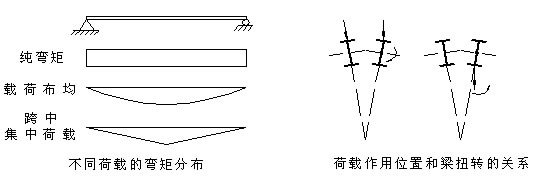
2.荷载作用位置
3.侧向抗弯刚度![]()
4.抗扭刚度![]()
5.侧向支承点间距![]() 。
。
6.梁的支承情况
五.提高梁整体稳定性的措施:
1.提高侧向抗弯刚度。(增大b)
2.提高抗扭刚度(增大b同样可以)
3.最有效的办法——加侧向支承,减小侧向支承点间距![]() 。支承加在受压翼缘有作用;满铺屋面板焊牢则不失稳。
。支承加在受压翼缘有作用;满铺屋面板焊牢则不失稳。
六.设计与计算:
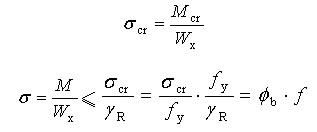
规范形式:
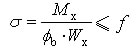
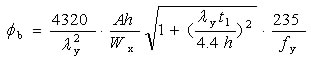
Wx——按受压翼缘确定的梁的毛截面抵抗矩;
λy——梁侧向支承点间对弱轴y—y的长细比;
t1——受压翼缘的厚度;
φb——梁的整体稳定因数。其通式为:
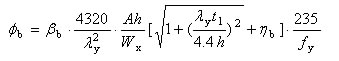
在使用公式应注意:我们前面推导过程中的前提是:双轴对称焊接工字形截面、简支梁、纯弯状态下、弹性屈曲。
1. 对于不同荷载及不同荷载作用位置情况应考虑与荷载种类及荷载作用位置有关的因数βb 。 βb与因数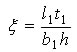 有关,查表;
有关,查表;
例如:跨中无支承,集中荷载作用上翼缘
![]()
![]()
详见规范附表1.1
2.对于单轴对称截面考虑不对称因数ηb 。
ηb与因数![]() 有关:
有关:
I1——受压翼缘对y轴的惯性距
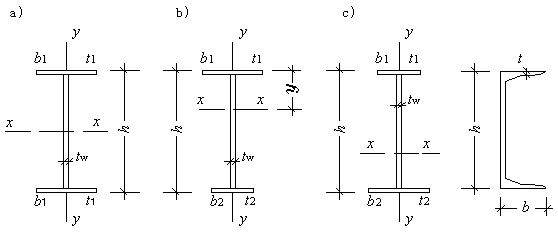
加强受压翼缘时:
加强受拉翼缘时:
双轴对称工字型:
3.轧制工字型钢,可直接查表
4.轧制槽型钢:
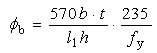
5.弹塑性阶段失稳,根据理论分析和试验,包括初弯曲,初偏心及残余应力的影响,得弹塑性稳定公式:
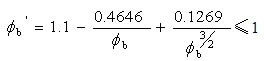
6.使用φb时,应按规范给定的最接近的情况采用,当实际情况和规范存在较大差异时,需自行推导临界应力值。
7.双向弯曲时:
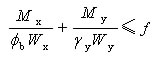 (经验公式)
(经验公式)
(2) γy为适当降低第二项的影响,决不是绕y轴允许发展塑性;
(3)此表达式在形式上与压弯构件相协调;
8.从概念出发,当φ'b ≥1时,不发生失稳现象,主要决定于
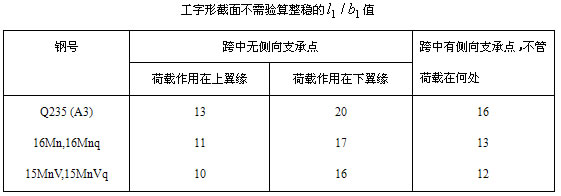
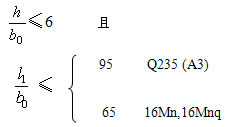
时,不必验算梁的整体稳定。
10.近似计算当
工字型截面:
双轴对称:
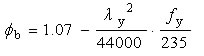
单轴对称:
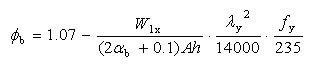
T型截面(弯矩作用在对称轴平面,绕x轴):
翼缘受压时,双角钢T形截面:
两板组合T形截面:
翼缘受拉时,φb =1
当 φb>0.6时,不必再进行修正。 φb>1时,取 φb=1。