图4-2 80%学习曲线图
企业的生产能力随着人们提高熟练程度的提高、设备和人员的增加，会产生新的生产能力。实践证明，这种生产能力的提高存在着某种规律性;在积累了一定的资料后，可相当精确地对以后生产的改进程度做出估计。这种规律被称为学习曲线。
学习曲线现象最早是20年代在美国一家飞机装配工厂被认识到的。该厂的研究表明。在产量成倍增加时，每一个倍增产品的直接人工总按20%递减。这样，如果飞机1花费10000小时，飞机2便花费8000小时，而飞机4则只花费6400小时。即是说，由于20%的递减率，意味着第4件产品所需的生产时间只是第2架产品的80%。这个累计产量和单件生产时间坐标的曲线，叫做“80%学习曲线”。如图4-2所示。
图4-2 80%学习曲线图
学习曲线现象给生产计划工作提供了一个重要的分析工具。可利用它来估计未来劳动力需要量和生产能力，估计成本和编制预算，制定计划和安排作业进度。学习曲线有三个假设：
1、完成一项给定任务或某个产品所需的时间将逐渐减少；
2、某个产品所需的加工时间按递减率随连续总产量增加而减少；
3、加工时间的减少，将遵循一个特定而可预计的进度模型。
在假设条件下，为利用学习曲线进行定量分析，需要将它表述为数学解析式。按上述的学习曲线现象所反映的规律，它的变化符合负指数函数关系：
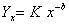（4.5）
式中：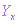
— 生产第x台产品的直接人工工时；
x — 生产的台数；
K — 生产第一台产品的直接人工工时；
b —
幂指数＝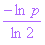
；
p — 学习率。
表4-3列出了常见的学习率下b的计算值。
表4-3 各种学习率下的幂指数值b
学习曲线可用于估计未来的劳动力需要量和生产能力，估计成本和编制预算，制定计划和安排作业进度。
[例4-2] 已知生产第一台产品的工时为10000小时，学习率为80%，求第8台产品的工时。
解：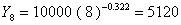 
（小时）。
当生产某产品的开始阶段，由于多种因素的干扰，不能得到确切的反映学习曲线效应的数据。这时，需要利用部分历史资料来估计学习率。此时，可先假设只收集到x1和x2两种产量的人工工时，则
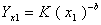
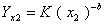
将两式相除，得
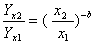
或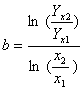 
再从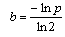
中求得p。
也可用学习曲线来估计一批产品的生产周期。在学习曲线下的产品总工时Hm是每台产品生产工时之和，即：
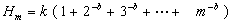
当产量足够大时，可假设Hm为连续函数，则有：
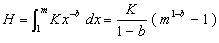（4.6）
学习曲线现象告诉我们，生产中永远有潜力可挖。但对于管理者来说，应该认识到，沿着学习曲线改进生产的过程不会自动发生。它不仅是工人个人改进生产的结果，而且是整个企业自觉努力的结果。在持续生产一种产品的过程中，企业总是要努力改进生产方法、改进产品设计、实施标准化、采用新工具、改善车间平面布置、以及改进管理工作，从而取得学习曲线的效果。不过，学习曲线原理主要适用于新产品，或具有很大改进潜力的生产过程;作为企业则应通过奖励或激励的措施，鼓励相引导员工来改进生产，促进学习曲线的实现。另外，学习曲线的代价是生产系统的刚性化，它会使得生产系统变得缺乏适应变化和更新产品的能力。因此，只有当产品定型,需求增长时，可能也有必要利用学习曲线来促进各部门不断提高生产效率。