|
观测精度的衡量
一、精度的含义
观测精度就是指误差的密集或离散的程度。假如两组观测成果的分布相同,便是指观测成果的精度相同;反之,若误差分布不同,则精度也就不同。
二、衡量精度的指标
为了衡量观测值的精度高低,可用组成误差分布表或绘制误差分布图的方法来比较。但在实际工作中,这样做不够方便,而且对精度得不到一个具体数字概念。为此,可采用能反映误差分布的密集或离散程度的具体数字来衡量精度的标准,这个标准称为衡量精度得指标。
1、中误差(均方误差)
在一定的观测条件下,各个真误差平方的平均数的平方根,称为中误差。中误差用m表示,即:  1-1 1-1
[例一]有一列观测值的真误差,分别为4"、
-2"、0"、-4"、3",求其中误差。
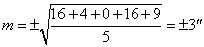 1-2 1-2
上例是根据观测值的真误差求得的中误差。真误差是由真值减去观测值求得,在一般情况下,一个量的真值是不知道的,因此,真误差也常不能求得。在实用中,通常是根据改正数来确定中误差的。
设对真值为x的某一量进行了n次同精度的观测,求观测值分别为:L1
L2 L2 ……Ln,相应的真误差为:Δ1、Δ2……Δn。故有:
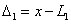
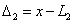
……
……
……
……
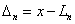 1-3
1-3
我们把算术平均值与观测值之差,称观测值的改正书,以v表示。于是又:
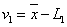
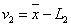
……
……
……
……
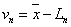 1-4
1-4
以上两式相减得:
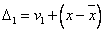
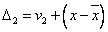
……
……
……
……
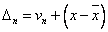 1-5
1-5
将1-5分别自乘后相加得:
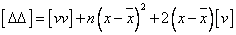 1-6
1-6
若将1-4中各式相加,有:
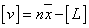 1-7
1-7
根据算术平均值的定义,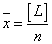 ,则上式可写成: ,则上式可写成:
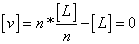 1-8
1-8
再将1-8代入1-7,有:
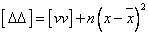 1-9
1-9
再将1-5之各式相加得:
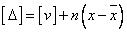 1-10
1-10
由于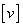 =0,所以 =0,所以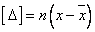 ,将此式自乘之,有: ,将此式自乘之,有:
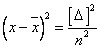
将上式代入1-9,可得
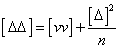
即
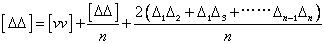
上式中,Δ1、Δ2、……Δn为偶然误差,在相当多的观测次数情况下,一部分显示为正,另一部分为负,这样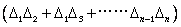 中之值有正也有负,其中大部分互相抵消,在除以观测次数n,其值更小,可忽略不计。于是上式可写成: 中之值有正也有负,其中大部分互相抵消,在除以观测次数n,其值更小,可忽略不计。于是上式可写成:
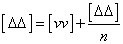
即
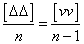 1-11 1-11
将1-11代入1-1,则得到以改正数求观测值中误差的公式:

2、相对误差
相对误差K是中误差的绝对值与相应观测值之比。
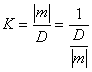
3、极限误差
偶然误差的第一个性质指出:在一定的观测条件下,偶然误差的绝对值不会超过一定限值。因此,如果能在观测之前确定出这个限值,那么便能使观测值达到预先所规定的精度。问题是如何确定这个限值?根据对大量观测数据的统计分析,并且参考误差理论得占总数的5%;大于三倍中误差的偶然误差,仅占总数的0.3%。
在实际工作中,观测的次数总是不会太多的,因此,通常认为大于三倍中误差的偶然误差,实际上是不可能的。故一般取三倍中误差作为误差的限值,称为极限误差。表示为:
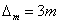
由于国家等级控制测量对观测精度要求比较高,故而规定两倍中误差为极限误差,表示为:
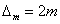
上述两式中,m为观测值的中误差,是一个具体的数字。当中误差确定后,所取极限误差也被确定。所以,在测量工作中,如果发现超过此限值,则该测量结果不能采用,必须予以重测。 |



