|
法国革命爆发不久,柯西(Augustin—Louis Cauchy,公元1789—1857年)诞生了.父亲曾是王朝时代的高级官吏,由于“革命”使他受到沉重打击,随时有被杀害的危险.过着隐居的生活.柯西在这种社会环境中,度过了童年时代.
后来,柯西的家境终于有了转机,柯西也得到了到鲁塞(Lycee)学校(法国中等学校,毕业考试合格,可获学士学位)学习的机会.学习认真刻苦,一丝不苟,给来防的数学家以深刻的印象.著名数学家拉格朗日曾面带笑容留心观察这位少年的举止言行,拍着他的肩膀对数学家拉普拉斯说:这位少年,将成为我们后继的数学家.
柯西于1805年进入理工科大学,1807年毕业,以第一名的优异成绩毕业后,又进入土木工程学院(Ecole desponts et chaussees),于1810年毕业.1814年8月22日在巴黎科学院宣读了“关于定积分”的论文,到了1825年才印刷出版.数学家拉克鲁瓦和拉格朗日对柯西的工作给予了相当高的评价.
柯西于1815年在多科工艺学校和巴黎大学讲授解析学.1816年发表了关于液体表面波传播理论的文章,获得了巴黎科学院的最高科学奖.
柯西以顽强的精神研究数学,创建了许多业绩,在遗留下来一万多页涉及各个领域的成果之后,于1857年5月23日逝世.
柯西为解析学的发展做出了重要贡献,他是从发展“函数定义”来创建解析理论的.柯西在1820年撰写的名著《解析学讲义》中,阐述了“如果两个变量,给出其中一个变量的值,就可确定另一个变量的值,则把前一个变量叫作自变量,后一个变量叫作塔的函数”.根据这个定义,揭示了函数概念的关键是确定两个变量对应关系,这是划时代的贡献.
从柯西定义的“函数”概念出发,可得到无穷小量的解析定义,以致对无穷小的计算成为可能,并应用无穷小定义揭示“连续”概念.
柯西《微积分学概论》,揭示了“若函数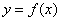 在给定的范围内是连续的,当变量 在给定的范围内是连续的,当变量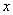 在此范围内给一个无限小的增粮时,函数也随之产生了无限小的增量,当增量 在此范围内给一个无限小的增粮时,函数也随之产生了无限小的增量,当增量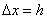 时,其差比为: 时,其差比为:
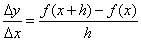 ” ”
若分子、分母都无限趋近于0,而其比收敛于一正值或者一负值,也就是说极限值存在,并对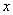 的每一个确定的值,都存在相应的极限值.由函数定义可知,这个极限值时 的每一个确定的值,都存在相应的极限值.由函数定义可知,这个极限值时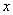 的函数,把这种新函数叫作导函数.进而,又产生了“可微分”的概念.向地道的分析学迈出了可喜的一步. 的函数,把这种新函数叫作导函数.进而,又产生了“可微分”的概念.向地道的分析学迈出了可喜的一步.
由牛顿和莱布尼茨创立的“积分法”,没有建立严格的理论基础,即使在18世纪之后,欧拉以计算发展了积分法,也没有奠定严格的理论基础.到了19世界之后,才形成了较完整的理论系统.对此做出卓越贡献的,就是我们崇敬的柯西.

|
