§2.3 母线平行于坐标轴的柱面方程
假设动点![]() 的坐标间的关系是不含变数
的坐标间的关系是不含变数![]() 的方程
的方程
![]() (1)
(1)
在![]() 平面上,这方程表示一条曲线
平面上,这方程表示一条曲线![]() ,这曲线
,这曲线![]() 上的点的坐标满足这方程。假定
上的点的坐标满足这方程。假定![]() 上的一点
上的一点![]() 对于
对于![]() 平面上的平面坐标系的坐标是
平面上的平面坐标系的坐标是![]() ,那么点
,那么点![]() 在空间坐标系里的坐标是
在空间坐标系里的坐标是![]() ,显然
,显然![]() 满足(1),因此
满足(1),因此![]() 点在曲面(1)上,从而曲线
点在曲面(1)上,从而曲线![]() 上各点均在(1)所表示的曲面上。不仅如此,自
上各点均在(1)所表示的曲面上。不仅如此,自![]() 作
作![]() 轴的平行线
轴的平行线![]() ,并于其上任意取一点
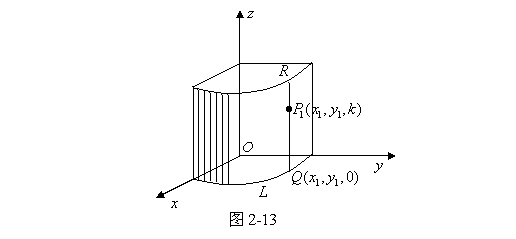
,并于其上任意取一点![]() (图2-13)。假定
(图2-13)。假定![]() ,那么点
,那么点![]() 的坐标是
的坐标是![]() ,容易知道
,容易知道![]() 满足(1),因此
满足(1),因此![]() 也在曲面(1)上,从而整个直线在曲面(1)上;反过来,如果
也在曲面(1)上,从而整个直线在曲面(1)上;反过来,如果![]() 在曲面(1)上,那么有
在曲面(1)上,那么有
![]()
所以![]() 在平行于
在平行于![]() 轴且过曲线
轴且过曲线![]() 上的点
上的点![]() 的直线上。所以曲面(1)是由平行于
的直线上。所以曲面(1)是由平行于![]() 轴的直线沿曲线
轴的直线沿曲线![]() 移动而成,这样的曲面叫做柱面,曲线
移动而成,这样的曲面叫做柱面,曲线![]() 叫做它的准线,形成柱面的动直线叫做它的母线。因此方程
叫做它的准线,形成柱面的动直线叫做它的母线。因此方程![]() 决定一个母线平行于
决定一个母线平行于![]() 轴的柱面。
轴的柱面。
同理,![]() 与
与![]() 都表示柱面,它们的母线分别平行于
都表示柱面,它们的母线分别平行于![]() 轴与
轴与![]() 轴。
轴。
例如方程
![]() (2.3-1)
(2.3-1)
![]() (2.3-2)
(2.3-2)
![]() (2.3-3)
(2.3-3)
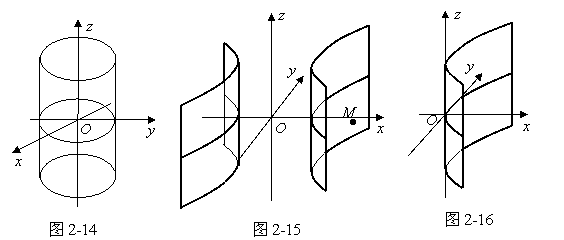
分别表示一个柱面,母线平行于![]() 轴,它们在
轴,它们在![]() 平面上的准线分别是椭圆、双曲线和抛物线,所以分别叫做椭圆柱面(图2-14),双曲柱面(图2-15)与抛物柱面(图示2-16)。它们的方程都是二次的,所以都叫做二次柱面。
平面上的准线分别是椭圆、双曲线和抛物线,所以分别叫做椭圆柱面(图2-14),双曲柱面(图2-15)与抛物柱面(图示2-16)。它们的方程都是二次的,所以都叫做二次柱面。