3．比较与决策

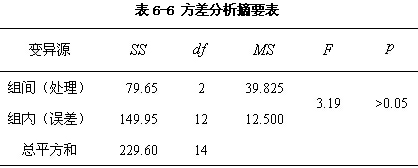
当组间自由度为2，组内自由度为12时，。因为，＜，＞0.05，差异不显著，接受虚无假设，拒绝研究假设，说明三种单词记忆方式之间没有显著差异。

4．方差分析摘要表

三、方差分析中的多重比较

方差分析中通过F检验，完成的是对多个平均数间差异的综合性检验，它只能综合判断各总体平均数间是否有差异。如果F检验的结果是各平均数间差异不显著，则各组平均数相等，检验分析工作结束；如果F检验表明各样本所来自的总体平均数之间差异显著，说明各平均数间至少有一对不等，但并不意味着每对平均数之间都有差异，究竟哪对平均数相等，哪对平均数不等，并不完全清楚。这就需要对平均数作进一步的逐对比较，进而确定哪两个平均数之间有差异，哪两个平均数之间没有差异，这就是平均数间的多重比较。

事后检验就是比较每一个处理组与另一个处理组, 一次比较两个，这称为成对比较。 这样的做法有没有问题？

每一个比较都是一个单独的假设检验, 每一个都有犯I类错误的风险. 所以,比较对数越多, 作结论的风险越大。即容易发现实际不存在的差异。 这称为实验导致的（experimentwise）alpha 水平 (或族系（familywise） 误差)

αEW = 1 - (1 - a)c    c = 比较对数

对于上述例子, 如果选择 a = 0.05 作3 对比较

αEW = 1 - (1 - a)c = 1 - (.95)3 = 1 - .857 = .143

I类错误的机会增加到14.7%而不再是5%，多数事后检验设计中都控制了实验导致误差。方差分析可以对多个均值是否相等进行检验，这是其长处。当拒绝时，表示各均值不全等，但具体哪一个或哪几个均值与其他均值显著不同，或者哪几个均值仍然可能认为是相等的，方差分析就不能给我们答案了，如果要进一步分析，可以采用多重比较的方法。

多重比较是通过对总体均值之间的两两比较来进一步检验到底哪些均值之间存在差异，总共要作次比较。 多重比较方法有十几种，请参考教材相关章节，这里不再一一介绍。