无限循环小数 教学内容：《现代小学数学》第八册——无限循环小数 教学目的:  1.使学生理解无限循环小数的概念,掌握循环小数的简便记法。  2.使学生具有判断纯循环小数和混循环小数的能力。  教学过程:  1.检查复习。  (1)把下列分数化成小数。 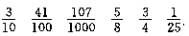 　 学生逐个回答后教师提问。  师:如何判断一个分数能否化成有限小数?  生:一个分数的分母只含质因数2或5,这个分数才能化成有限小数。  师:你知道这是为什么吗?  生:当分母只含质因数2或5时,根据分数的基本性质,分子、分母同乘以2或5,就能得到分母是10、100、1000的分数,也就能化成有限小数。例如 17/50 ,分子、分母同乘以2,就是34/100 化成小数是0.34。  师:那么不能化成有限小数的分数,可以化成什么样的数呢?今天就来研究这个问题。  (这种自然地过渡,不仅符合事物之间的内在联系,也具有激发学生探讨新问题的功能。)  2.新课。  (1)关于无限循环小数。  师: 8/11、2/9、5/12 和 9/55 都不能化成有限小数,我们看一看,究竟能化成什么样的小数呢?拿 8/11 来说,根据分数与除法的关系,可以列成什么样的算式?  生：8/11=8÷11。 教师板演：  师:继续除下去会怎么样?  生:还是先商7,再商2。  师:你怎么能肯定会得出这样的结果呢?  生:开始时商7余的是3,商2余的是8,后来又商7余3,又商2余8。如果再除还得先商7,再商2。  师:继续除下去商一定重复,简单地说是从哪儿看出来的呢?  生:余数重复出现。 师:8/11 化成小数是0.7272……，有多少个“72”呢？  生:有无数个。  师:既然是无数个,我们可以怎样表示?  生:使用省略号。  教师要求学生分组计算，求出 2/9、5/12 、9/55 化成小数的结果。学生求出  2/9 =0.22…… 5/12 =0.4166……  9/55 =0.16363……  教师逐个提问省略号所表示的是什么。  师:不能化成有限小数的分数,化成的小数可以用省略号表示,表示它们的位数是无限的。这样的小数,由于位数是无限的,所以叫无限小数。  教师板书:无限小数  师:无限小数的小数部分有什么特点?  生:有的是一个数无限循环。  生:有的是两个数无限循环。  师:小数部分一个数字或者几个数字依次不断重复出现,这样的小数叫无限循环小数。  练习：下列哪些小数是无限循环小数?  (1)0.999……  (2)4.1677……  (3)52.052052……  (4)3.212121  (5)3.1415926  学生回答后教师提问。  师:前三题,大家判断一致,现在研究4、5两题。第4题为什么不是无限循环小数?  生:第4题是有限小数。  师:第5题呢?  生:小数部分没有重复的数字,所以不是无限循环小数。  (抓住无限循环小数的本质属性设计练习,可以克服学生理解中的片面认识。题目虽少,但作用甚大。)  (2)关于循环节及循环小数的简便记法。  师:小数部分依次不断重复出现的数字叫循环节。例如:  0.7272……的循环节是什么?  生:72。  师:0.222……的循环节呢?  生:2。  师:0.4166……的循环节呢?  生:6。  师:0.16363……的循环节呢?  生:63。  师：3.2041041……的循环节呢?  生:041。  随着学生的回答。教师把每个数的第一个循环节用彩色粉笔框起来。  师:循环小数可以这样表示,把循环节写出两遍或三遍,然后点上省略号。不过这样写比较麻烦,简便的写法是循环节只写一个。像3.2041041……,循环节只写一个是3.2041,这样写行吗?  生:不行,它们并不相等。  师:又想简便,又要数值不变,可以这样写：在循环节的首位和末位上各记一个圆点,也就是循环点。例如3.2041041……用循环节的方法表示是  ,读作三点二零四一,零四一循环。  师20.16363……怎么样简写?  生:写成零点一六三,六三循环。  师:我们再练习几个,用简便记法表示下列各循环小数。  0.00505……  8.1010……  3.101101……  学生在本上练习,个别人写在玻璃片上,然后教师通过幻灯进行订正。  师:  用一般方法又怎么写?  生:0.0202……  (3)关于纯循环小数与混循环小数。 师:(指着 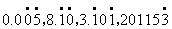  四个循环小数提问。)小数部分有没有区别?  生:有的从小数点后面第一位起循环,有的从第二位起循环,有的从第三位起才循环。  师:根据这种区别又可把无限循环小数分为两种:一种是从小数点后面第一位起就循环的,叫纯循环小数(板书:纯循环小数)；另一种不是从小数点后面第一位开始循环的,叫混循环小数(板书:混循环小数)。  也就是说,分数化成小数,有两种情况,一种是有限小数,另一种是无限循环小数。而无限循环小数,又有两类,一类是纯循环小数,另一类是混循环小数。  师:谁能举几个纯循环小数的例子?  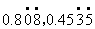生: 师:谁能举几个混循环小数的例子 生: 师:你们知道什么样的分数能化成纯循环小数,什么样的分数能化成混循环小数吗?  (学生有些困惑)  师:一个分数能否化成有限小数,我们看哪儿?  生:看分母。  师:现在还来分析一下分母。  (学生分组议论)  生:分子、分母互质的时候,能化成纯循环小数。  生:不对,5/12 的分子分母也互质,可化出来的是混循环小数。  生：化成纯循环小数的分数,分母只含2、5以外的质因数；能化成混循环小数的分数,分母含2或5中的一个,还有其它的质因数。  师：化成纯循环小数的分数,分母只含2、5以外的质因数,能化成混循环小数的分数,分母除含质因数2或5外,还含有其它的质因数。  分母的质因数数中有2或5,就存在着把分母化成10、100、1000的条件,又有其它质因数,就又存在着分母化不成10、100、1000的条件,所以一定是化成混循环小数了。  师：现在我们来判断一下,下列各个分数能化成纯循环小数还是混循环小数。 5/14、5/2、4/15、6/13 学生回答后,教师小结。  师:这节课学习,无限循环小数,认识了循环节以及循环小数的简便记法,并且也知道,无限循环小数又可分为两类。都掌握了吗?现在我来考考你们。  1.下列各数能否用等号连接?请用反馈板来回答。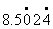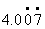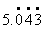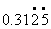  ① 8.5024024……=  ② 4.00707……= ③ 5.043043……= ④ 0.32525……=  学生用反馈板逐个回答。问题主要表现在第③题上,教师又组织学生讨论,大家一致认识到5.043043本身是有限小数,所以与5.043并不相等。 2.下列各数都是纯循环小数吗?请用反馈板来回答。 ① 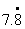    ②  [upload=gif]UploadFile/200362321313972316.gif[/upload  ③ ] 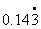   ④ 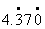    ⑤ 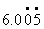  (使用反馈板是个好方法,该班学生每人有2块,一块标明“√”,一块标明“×”。在判断练习中,学生的认识立即用反馈板表明出来,教师也就马上掌握了学生的理解状况。只有及时反馈，教师才能根据实际情况,调整教学进度或改变教学方法,以争取达到最佳的教学效果。)  3.质疑。  师:这节课我们把分数化成小数的另外一种情况研究完了。上节和这一节,所研究的中心都是分母含质因数的状况。清楚了这一点,也就提高了我们的认识能力和判断水平。大家还有什么问题?  生: 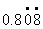为什么不写成 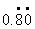？ 师: 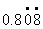 也就是0.8080808……，写成 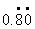？可以不可一？ 生:可以。  师:一个纯循环小数,可以写成混循环小数。当然,像 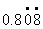最好还是写成 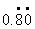。 生:分数化成小数有两种情况,一种是化成有限小数,另一种是化成无限循环小数。能不能化成无限不循环小数呢?  师:你们说呢?(学生思考一下后教师接着讲)分数化小数时是用分子除以分母。做除法时,余数一定要比除数小,也就是说余数的数值是有限的。例如8/11,当8除以11时,余数最大是几?  生:是10。  师:就算前面的余数表示重复,第11次余谁呢?余数肯定就重复了,余数一重复,商也就重复了。所以不可能得到无限不循环小数。  (学生问得好,教师回答得也好,好就好在是在师生共同的研讨之中。)