1 . (1)
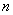
|
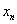
|
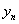
|
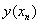
|
欧拉法 |
预估-校正法 |
0 |
0 |
1 |
1 |
1 |
1 |
0.1 |
0.9 |
0.91 |
0.909674836 |
2 |
0.2 |
0.82 |
0.83805 |
0.837461506 |
3 |
0.3 |
0.758 |
0.78243525 |
0.781636441 |
4 |
0.4 |
0.7122 |
0.741603901 |
0.740640092 |
5 |
0.5 |
0.68098 |
0.71415153 |
0.713061319 |
(2)
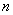
|
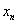
|
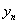
|
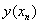
|
欧拉法 |
预估-校正法 |
0 |
0 |
1 |
1 |
1 |
1 |
0.2 |
1.2 |
1.186666667 |
1.183215957 |
2 |
0.4 |
0.1373333333 |
1.348312254 |
1.341640786 |
3 |
0.6 |
1.531495145 |
1.493703893 |
1.483239697 |
4 |
0.8 |
1.681084569 |
1.627861081 |
1.61245155 |
5 |
1 |
1.82694818 |
1.754204635 |
1.732050808 |
2 .
( 1 )
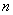
|
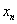
|
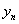
|
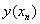
|
0 |
0 |
1 |
1 |
1 |
0.2 |
0.837466667 |
0.837461506 |
2 |
0.4 |
0.740648541 |
0.740640092 |
( 2 )
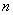
|
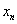
|
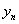
|
0 |
1 |
1 |
1 |
0.1 |
1.240119836 |
2 |
0.2 |
1.587342907 |
3 .解应用泰勒展开式得
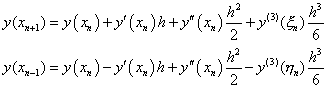
两式相减得
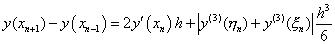
略去误差项,对 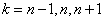 ,用 ,用 
则有 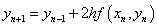
它的局部截断误差为
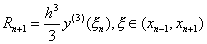
4 .提示:证明 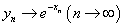 时,对 时,对 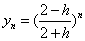 ,再应用罗比达法则证 ,再应用罗比达法则证
明.
5 .提示:
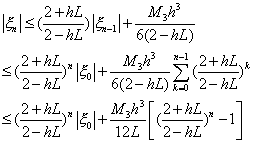
当 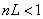 时, 时, 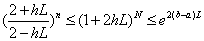
6 .解:将改进欧拉法用于实验方程
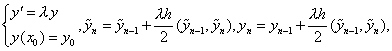 两式相减得 两式相减得 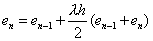
整理得 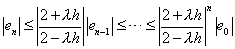
当 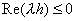 时,则有 时,则有 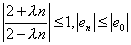 , ,
所以改进欧拉法的绝对稳定域为 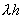 复平面的整个左半平面。 复平面的整个左半平面。
|