2-1-1-1 LCAO—MO法

所有分子中最简单的是H离子、因为它有两个核但只有一个电子。如能找到可以用来描述一个电子在这类二中心场中运动状态的一些轨道，就有可能完全与一中心场情况一样，导出双原子分子的构造原理（aufbau theory），进而推广到多中心场的情况。这种遍及所有核上的单电子轨道称为分子轨道(MO)；在晶体中称为晶体轨道。在这近似法中，电子按能量递增的次序填入各相应的分子轨道，以这样的近似法得到的总电子密度也正好等于各轨道贡献之和。

最简单的途径是从原子轨道组成分子轨道，取：

ψ=C₁+C₂+C₃+…

式中、…等是所用的原子轨道(AO)，分别附加系数c₁、c₂…。这方法称为原子轨道线性组合(LCAO)近似法。

对于H，这样的一个近似MO就是ψ=C_a+C_b,这里和是核a和b的1s轨道。因为AO的函数是按指数减小的。所以，在靠近核a某点的ψ基本上是C_a，它是一个电子与核a结合在一起时波动方程的解。同样，电子靠近核b时ψ的状态以C_b表示。因此尚需确定C_a和C_b值。对此，有标准的数学方法，不仅能解出H最低能态的系数和能量，而且能解出与原子轨道数目同样多的能态的成组系数和能量。这里,H中的两个中心是相同的，发现电子的几率P=ψ²是对称的，这意味着C_a= +C_b，因而这两个解是：

ψ₁=N₁(+) 和 ψ₂=N₂(-)

式中N₁和N₂为归一化常数。以LCAO法得到的分子轨道ψ₁、ψ₂，它们沿核a和b轴的数值以及相应的电子密度分布如图2-2所示。

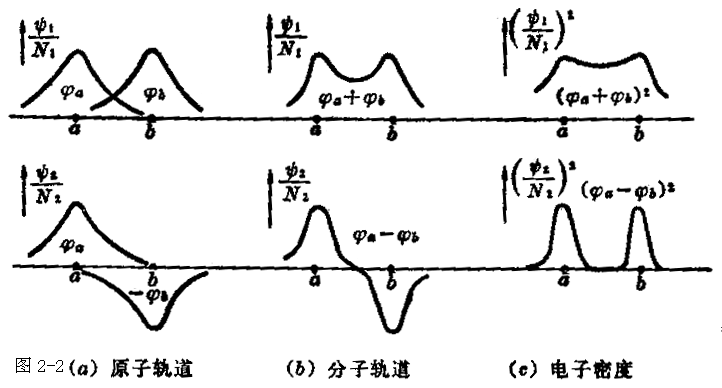
很明显，在核a和b之间有相当大的电子密度，它与成正比，但在a和b的中间电子密度为零，这些分子轨道的形状如图2-3所示。这两个分子轨道称为成键轨道和反键轨道；它们是由1s原子轨道组成，用σ_1S和σ^*_1S表示，这里σ表示分子轨道对称于分子轴，星号代表反键MO，以区别于成键MO。

与原子轨道一样，二中心波动方程解的组数是无限的；σ_1s和σ_1s*是两个最低能量的解。有些解引出的某些分子轨道，有一个以上与键轴相交的节点。另一些解引出的分子轨道，含有通过两个核的节面，等等。所有这些分子轨道的主要特征都能用LCAO近似法很好表示出来。

MO的对称性可用包含分子轴的节面数来表示。含有0、1、2…个这种节面的分子轨道用符号σ、p、δ…来表示。这与AO用s、p、d符号表示相似。而且，这些节面数目与量子化的角动量(绕分子轴的动量)数值l(h／2π)相当，这里l=0、+1、+2…。因而，除了σ轨道外，其它类型的分子轨道存在着相当于电子在不同状态下运动的简并对；如π2p_x和π2p_y分子轨道，它们表示特定角动量的状态（l=+1）且由相同成份混合而成，与它们对应的原子轨道为2p_x和2p_y。

σ键（图2-4）：一对成键电子的电子云密度分布，对于两个原子核的联线—键轴,呈圆柱形对称。

π键（图2-5）：电子云分布的界面图象，对于通过键轴的一个平面对称，含有1个节面。

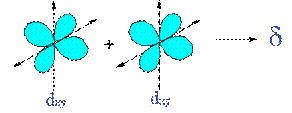
δ键（见右图）：电子云分布的界面图象，对于通过键轴的二个平面对称，含有2个节面。

思考题：σ、π和δ分子轨道的对称性特点都是什么？