6-2-2-3 π成键杂化方案
σ与π的区别:
σ键定义:没有包含键轴的节面的轨道
π键定义:有一个包含键轴的节面的轨道。
在ABn分子中,原子A上要有2n个π型杂化轨道和在B原子上的2n个π原子轨道成键。这两者应为分子对称群的同一表示的基。
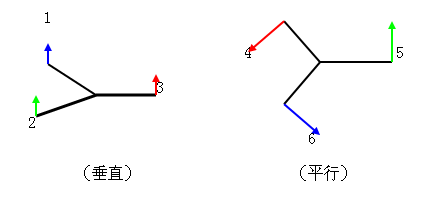
再者,B原子上的各个π原子轨道,可以用垂直于A-B连线并指向于波函数正值方向的一个向量来表示。每个B原子上有两个这样成直角的向量。
(1)以AB3(D3h)为例:
在平面分子的情况下,为方便起见,令B原子上一个向量垂直于分子平面,则另一向量必在分子平面内。

任何操作中,垂直于平面的向量不与平面内向量交换。
这说明每一组各自独立地得到一个表示:
|
D3h |
E |
2C3 |
3C2 |
σh |
2S3 |
3σv |
|
Γ(⊥) |
3 |
0 |
-1 |
-3 |
0 |
1 |
|
Γ(‖) |
3 |
0 |
-1 |
3 |
0 |
-1 |
根据D3h群特征标表(表6-1),利用约化公式将可约表示约化:
Γ(⊥)=A2″+E″
Γ(‖)=A2′+E′
为使A原子与每一个B原子形成一个垂直于分子平面的π键,它必须由属于A2″的一个原子轨道和两个属于E″的简并轨道构成杂化轨道。
由D3h特征标表,得:
|
A2″ |
E″ |
|
pz |
(dxz,dyz) |
因此可由(pz、dxz、dyz)组成一组等价的垂直于分子平面的杂化轨道。
再考虑π(‖)键:
|
A2′ |
E′ |
|
没有 |
(px、py) (dx2-y2、dxy) |
由于没有A2′对称性的原子轨道,因此不能形成一组三个等价的π(‖)键,但并不表示不能形成π(‖)键,也不表示只有两个B原子可以形成π(‖)键。它仅表示两个π(‖)键平均分配在三个B原子间。
在前面[HgI3]- ( D3h)的例子中我们已经得知具有E′对称性的原子轨道(px、py)和(dxy、dx2-y2)可参加σ杂化。若σ成键和π成键属于相同的表示,而属于该表示的有两个(或两组)轨道,则σ和π成键均可得到满足。但单纯在对称性基础上,对于哪一组属于σ成键或π成键的问题不能明确回答。