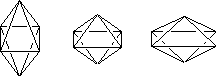
6-3-6 Jahn-Teller效应及配合物的畸变
1、Jahn-Teller效应
实验发现,6配位配合物并非均为理想的八面体构型。1937年,H.A.Jahn和E. Teller指出:在对称的非线型分子中,如果体系的基态有几个简并态,则是不稳定的,体系要发生畸变,以消除简并性。这就是关于配合物畸变的Jahn-Teller效应。它是在中心原子的电子构型含有不等性占有的简并轨道时都能发现的。
2、d9组态八面体配合物的Jahn-Teller效应
d9组态八面体配合物的电子排布为(t2g)6(eg)3:
╫ ┼ eg
╫ ╫ ╫ t2g
此类配合物有两种类型的畸变,伸长畸变和压扁畸变:
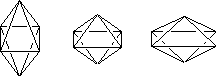
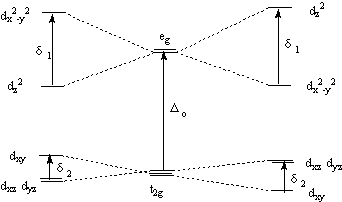
| 伸长畸变 | 理想八面体 | 压扁畸变 |
| (t2g)6(dx2-y2)1(dz2)2 | (t2g)6(dx2-y2)2(dz2)1 | (t2g)6(dx2-y2)2(dz2)1 |
| (t2g)6(dx2-y2)1(dz2)2 |
Δo >>δ1>δ2,总能量变化=(-1/2)δ1
3、不发生畸变的八面体配合物
如下d电子结构不会产生简并态,也就不会发生畸变,配合物将具有理想的八面体构型。
高自旋:
| d 0 | d 3 | d 5 | d 8 | d 10 |
| (t2g)0 | (t2g)3 | (t2g)3(eg)2 | (t2g)6(eg)2 | (t2g)6(eg)4 |
低自旋:
| d 0 | d 3 | d 6 | d 8 | d 10 |
| (t2g)0 | (t2g)3 | (t2g)6 | (t2g)6(eg)2 | (t2g)6(eg)4 |
总之:d 0、d 3 、d 8 、d 10组态及d 5高自旋和d 6低自旋态不发生畸变。
晶体场理论通过晶体场分裂能与成对能的关系解释了磁性。通过CFSE,可解释配合物的某些热力学及动力学性质。但难以解释为何中性配体(H2O、NH3)的晶体场分裂能Δ大于负离子(Cl-、Br-、OH-)的Δ。分子轨道理论将给出更定量的解释。