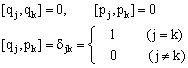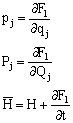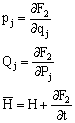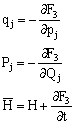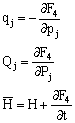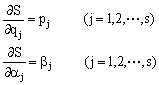|
当前位置:学习内容 -小
结 |
|||||||||||||||
|
小 结 I.哈密顿原理 1.变分运算的几个法则 变分符号用d表示,它和微分运算有许多类似之处。 对于等时变分(dt=0)而言,d与d的顺序可对易,即d(dr)=d(dr);d与
2.哈密顿原理(保守系适用)
其中 II.哈密顿正则方程 1.哈密顿函数H(qj,pj,t)
2.正则方程
3.如为保守系,且约束是稳定的,则 H = T + V = E 4.循环积分与能量积分 循环积分:H中不显含某个pj或qj,则对应的qj或pj为常数。 能量积分:H中不显含t,则H=E(稳定约束)或H=h(不稳定约束)。 III.泊松括号 1.泊松括号 (1) 定义 (2) 运动积分的判别式
2.泊松括号的性质 (1) [f,g]=-[g,f] (2) 若c为常量,则[f,c]=0 (3) [f1 + f2,g]=[f1,g] + [f2,g] (4) [f1f2,g]=f1[f2,g]+[f1,g]f2 (5) (6) 泊松恒等式 [f, [g, h]]+[g, [h, f]]+[h, [f, g]] = 0 (7) (8) 基本泊松括号
3.泊松定理 若f(qj,pj,t)=c1,g(qj,pj,t)=c2是正则方程的两个运动积分,则 [f,
g] = c3 也是正则方程的运动积分。 IV.正则变换 1.目的:希望通过变量变换,能得出更多的循环坐标,从而使问题简化。 2.条件: 3.几种形式的正则变换
V.哈密顿—雅可比方程 1.哈密顿—雅可比方程(H-J方程)
2.如R=S(qj,aj,t)+c是从上述H-J方程中求出的运动积分,则由
可求出正则方程的全部积分。 3.如为稳定约束,且H中不显含t,则S=-Et+V(q1,q2,…,qs,E,a2,…,as)+c,而H-J方程为
|
|||||||||||||||