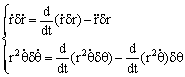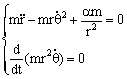当前位置：学习内容 -综 合 例 题

例7.1 试由哈密顿原理求质点在万有引力作用下的运动微分方程。[解] 在极坐标中，动能与势能分别为 （1）

故拉格朗日函数L为

(2)

代入哈密顿原理中得

(3)

但

(4)

把(4)式中的两个关系代入(3)式中，得

因 ,

而积分号内的dr和dq是任意的，即它们一般并不等于零，而且是独立的，故得

即

这就是我们所要求的关系。

例7.2 用哈密顿正则方程解单自由度线性振动问题。

[解] 取系统的一个广义坐标为q，则拉格朗日函数是

其中m为振子的质量，k为弹性系数(弹簧质量略去不计)。

广义动量是

由此算出哈密顿函数为

哈密顿正则方程为 ，

如消去p，则得方程。因为H不显含t，所以有广义能量积分

可见在相平面(q-p平面)上，相轨迹是一族椭圆，其中每一个椭圆的大小由总能量E决定。当然，相轨迹也可以从正则方程经消元得到，在正则方程中消去t，得

积分后得到的式子与能量积分是完全等价的。

上一页下一页