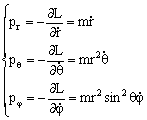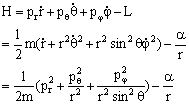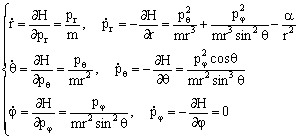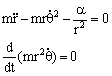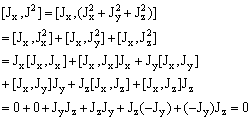当前位置：学习内容 –综合例题

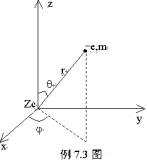
例7.3 设电荷为-e的电子，在电荷为ze的原子核所形成的库仑场中运动，z为原子序数。试用正则方程研究电子的运动。

[解] 这是三个自由度的运动，以场心为坐标系原点，选取球坐标(r，q，j)为广义坐标。如图所示，设m为电子的质量，则电子的速度平方为

动能为

势能为

拉格朗日函数为

因而得到广义动量为

(1)

哈密顿函数

把H代入正则方程中，得

(2)

这就是电子在核力场中的运动方程，因H中不含j，故，p_j=C=常数，而，由(2)的第一对方程及(1)，可得

(3)

由(2)式的第二对方程得 (4)

式(3)和(4)中都不含j，故知电子是在一平面内运动，由于电子所受的力是有心力，所以如果令此平面为j=0的平面，则，c=0，而电子在此平面内的运动方程为

例7.4 计算泊松括号[J_y，J_z]，[J_z，J_x]，[J_x，J_y]和[J_x，J²]，[J_y，J²]，
[J_z，J²]。式中J是角动量，即J=r´p。

[解] 先计算[J_y，J_z]。因为

J_y = zp_x – xp_z， J_z = xp_y – yp_x

利用泊松括号性质(3)则有
[J_y，J_z]=[zp_x – xp_z,xp_y - yp_x]
=[zp_x,xp_y] – [zp_x,yp_x] – [xp_z,xp_y] + [xp_z,yp_x] (1)

再利用性质(4)等式右边第一个泊松括号为

[zp_x,xp_y] = zx[p_x,p_y] + z[p_x,x]p_y + x[z,p_y]p_x + [z,x]p_yp_x

由基本泊松括号可知右边只有第二个括号为-1，其它均为零，因此有

[zp_x,xp_y] = - zp_y (2)

同理可得

(3)

把(2)和(3)式代入(1)式，最后得到 [J_y, J_z] = yp_z - zp_y = J_x

同理可得 [J_z, J_x] = J_y， [J_x, J_y] = J_z

下面计算[J_x, J²]

同理可证 [J_y，J²] = 0，[J_z，J²] = 0

上一页 下一页