位置：第四章第一节
(2)符号原理。如果学生掌握了适合于他们智力发展的符号，那么就能在认知上形成早期的结构。数学中有效的符号体系使原理的扩充和新原理的创造成为可能。例如，当表示方程的符号形成之后，就能学习解多项式方程的一般方法。布鲁纳认为，对于中学低年级的学生，表示函数的最好方法是使用以下的符号：□=2△+3,其中□和△代表自然数。逐渐地用y=2x+3来表示函数，最后用y=f(x)表示函数。布鲁纳认为，应当用螺旋式的方法来建构数学中的符号体系。这里的螺旋式方法指的是以直观的方式引进每一个数学概念，并使用熟悉的和具体的符号表示数学概念的方法。简单地说，符号原理就是要根据学生的智力发展水平，使其达到相应的抽象水平。
(3)比较和变式原理。比较和变式原理表明，从概念的具体形式到抽象形式的过渡，需要比较和变式，要通过比较和变式来学习数学概念。例如，在几何中，比较圆的弧、半径、直径和弦，能使学生对这些概念理解得更清楚。况且有些概念本身就是通过比较定义的，例如，负数是正数的相反数，不是有理数的那些数称为无理数。布鲁纳认为，比较是帮助学生直观地理解数学概念和发展其抽象水平的最有用的方式之一。
(4)关联原理。关联原理指的是应把各种概念、原理联系起来，置于一个统一的系统中进行学习。在数学教学中，教师不仅要帮助学生发现数学结构间的差别，而且也要帮助学生发现各种数学结构间的联系。布鲁纳认为，如果要使学生的学习卓有成效，就必须说明和理解数学概念间的联系。
布鲁纳的教学和学习理论，对我们有如下几点启示：
(1)在数学教学过程中，不仅应使学生掌握数学知识的概念、定理、公式等，还应理解数学知识的来龙去脉，应注重知识的产生过程，而不是孤立地记住一些数学结论。
(2)在表示数学知识时，要根据学生的情况，考虑是通过一系列实例呢，还是通过一些概念和原理，或是一系列符号。例如，在中学低年级，函数概念只能这样来表示：把米换算成尺；产量不变，总产量和亩数。稍高一点的年级就可用下面的例子来表示函数概念了：一系列物体的有序对，y=2x,y=
等。到高中，可以下述形式给出函数概念：y=f(x)是x的函数，如果集合X中的每一个元素a在Y中存在唯一的元素b和它对应，使得b=f(a)。
(3)在数学教学过程中，应把学习过的数学知识按一定的方式构造好，以便于学生记忆和保持。
(4)为了“迁移”做好充分的准备，应使学生对数学基本原理有深刻的理解，从而根据原理的结构，把掌握的模式应用到类似的事物中。例如，学生掌握了完全平方公式
的结构和特征，就可以利用此公式把下列二元三次式化成完全平方式
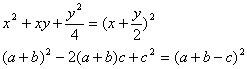
(5)要使学生享受到数学智力活动的乐趣，把从中得到的愉悦作为鼓励学生学习的重要手段。
二、认知——接受理论和数学学习
20世纪50年代，许多数学教育工作者认为，在数学教学中普遍应用的讲授法会导致学生的机械学习，而发现学习，探究学习是促进有意义学习的好方法。因此，许多人否定了讲授法在学校教学中的地位，只有部分人认为，讲授法在过去曾经起过良好的作用，今天不应把它作为不好的教学方法抛弃。正是在这样的形势下，美国心理学家奥苏伯尔提出了有意义学习理论。他的理论属于认知心理学范畴，但他不象布鲁纳那样强调发现学习，而是强调有意义的接受学习。因而他的理论可以称为认知——有意义接受学习理论。
奥苏伯认为，学习过程是在原有认知结构基础上，形成新的认知结构的过程；原有的认知结构对于新的学习始终是一个最关键的因素；一切新的学习都是在过去学习的基础上产生的，新的概念、命题等总是通过与学生原来的有关知识相互联系，相互作用条件下转化为主体的知识结构。
奥苏伯尔为了说明他的有意义学习理论，把学习从两个维度上进行划分：根据学习的内容，把学习分为机械学习和有意义学习；根据学习的方式，把学习分成接受学习和发现学习。
机械学习是指学生并未理解由符号所代表的知识，仅仅记住某个数学符号或某个词句的组合。例如关于函数符号y=f(x),学生可能知道这是函数的符号，也知道y代表因变量，x代表自变量，但它真正的含义并不十分清楚。表现在不能识别R→R: y=f(x)=x²和 u=f(v)=v²是同一个函数。或者会背函数的定义，但不知其意义，这些都是机械学习的表现。
“有意义学习过程的实质，就是符号所代表的新知识与学习者认知结构中已有的适当知识建立非人为的(非任意的)和实质性的(非字面的)联系”。这里所谓的非人为的联系，就是符号所代表的新知识同原有知识的联系。例如，要使对数概念的学习成为有意义的学习，就要把对数概念与指数概念、开方概念、实指数幂的性质等建立联系，即建立所谓的非人为的联系。所谓实质性的联系，指用不同语言或其他符号表达的同一认知内容的联系。例如对数概念，“㏒
b”；“求以a为底b的对数就是求a的多少次方等于b”；
三者表示的是同一个意思。这三者的联系就是实质性的联系。
