位置:第四章第三节
|
第三节 数学学习的迁移 |
学习能够迁移,这是学习中的普遍现象。例如学好数学,有助于理化的学习,学习了方程的知识,有利于不等式的学习。有关学习迁移的认识,在我国已有很长历史,早在两千多年前,孔子就指出:“举一隅不以三隅反,则不复也”“回也,闻一以知十”。意思是说学习可以“举一反三”、“触类旁通”,使学生达到“由此及彼”。对学习迁移的发生最早的系统解释是18世纪的形式训练说,第一次把迁移问题作为教育问题的核心提到日程上来的是美国心理学家布鲁纳。之后,学习迁移受到各国心理学家和教育家的关注,甚至把它作为一个教育教学的原则,提出要“为迁移而教”。
数学教育的目的是为了让学生牢固地掌握基本技能和发展学生的能力、态度,以其对学生的学习、走出校门后的学习和工作奠定。从这种意义上来说,数学教育的目的无非是举一反三,追求一种学习对另一种学习的促进作用。因此在数学学习中研究迁移问题,有其特殊、深刻的意义。
一、迁移的一般概念
学习的迁移是指学习者所习得的学习结果对其他学习的影响。在学习过程中,先前的学习会影响到以后的学习;同时,后面的学习有时也会影响以前的学习。我们把前者叫做顺迁移,后者叫逆迁移。学习中已获得的学习结果对其他学习的影响可能是积极的,也可能是消极的。那些起积极的,促进作用的影响叫做正迁移;起消极的抑制作用的影响,叫做负迁移。
在数学学习中,产生正迁移的现象是很多的。如学习方程的知识有助于学习不等式;学习数的运算规则有助于学习“式”的运算规则。象这种迁移在心理学上称为顺向正迁移。若后面的学习反过来能巩固、促进先前的学习,这种迁移称为逆向正迁移。例如,学习了解析几何以后学生重新来思考平面几何中的一些问题就变得容易了。
在数学学习中也会产生负迁移。例如,学习了解方程以后,学生掌握了“方程两边同乘以一个不等于零的数或式,方程的解不变”这一解方程的原理,往往会套用到解不等式中去,作为解不等式的原理,这就产生了顺向负迁移。把数集扩充到有理数后,学生学习有理数的减法会对算术减法产生负迁移,学生在做5-3时,也应用“减去一个数等于加上这个数的相反数”法则来进行5-3=5+(-3)=2这就是逆向负迁移。
根据上面的分析,关于数学学习的迁移可作如下分类:
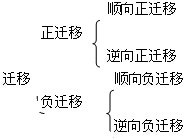
二、迁移现象的本质
数学教育的目标归根到底是为了达到正迁移,因而搞清楚迁移的实质对于数学教学中最大限度地实现迁移有着重要的意义。
心理学历史上,存在着各种学习的迁移理论:形式训练说,相同要素说,概括化理论,以及现代认知心理学从认知结构出发的迁移理论。尽管各种理论各自有其片面性,但他们有着其可鉴借之处。
1、形式训练说
该学说认为,多是通过对组成心智的各种官能的训练,以提高各种能力如注意力、记忆力,推理能力,想象力等而实现的。人的心智是由“意志”、记忆、“思维”、“推理”等官能组成的。学习要收到迁移的效果,就要经历“形式训练”,使之在不同的学习中认出形式上相似的东西。按照形式训练说的观点,数学教学中让学生做难题,则是训练“心智”的好方法,这能让学生学会观察、分析、比较,比记住一些具体知识更有益。但形式训练说片面地强调了“形式”,而低估了实在内容的价值。
2、相同要素说(共同要素说)
该学说是19世纪末,20世纪初桑代克提出的。相同要素说认为,一学习之所以有助于另一学习是因为两种学习具有相同因素的原因。若两种情境含有共同因素,不管学习者是否觉察到这种因素的共同性,总有迁移现象发生。
3、概括化理论
和桑代克同时期的贾德提出迁移的概括化理论。该理论认为,两个学习活动之间存在的相同要素,只是产生迁移的前提,而产生迁移的关键则是学习者在两种活动中概括出它们的共同原理,例如,学生在学习解二元一次方程组时,获得了“消元”这一解二元一次方程组的一般原理,紧接着在学生解三元一次方程组时,如果学生能把“消元”和解三元一次方程组联系起来,那么就能把解二元一次方程组的一般原理“消元”迁移到解三元一次方程组中去。