设实函数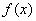 在区间[a,b]上单调连续,有数学分析知道,如果满足 在区间[a,b]上单调连续,有数学分析知道,如果满足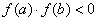 ,则方程 ,则方程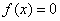 在区间[a,b]内有唯一实根 在区间[a,b]内有唯一实根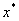 。 。
区间二分法基本思想是:将方程根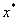 所在区间[a,b] 平分为两个小区间 ,再判断那一个区间是有根区间,即 所在区间[a,b] 平分为两个小区间 ,再判断那一个区间是有根区间,即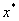 属于哪个区间;把有根区间平分为二,再判断 属于哪个区间;把有根区间平分为二,再判断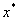 所在的更小的区间等等;重复上述步骤,直到求出满足精度要求的近似根,如图8-1所示。 所在的更小的区间等等;重复上述步骤,直到求出满足精度要求的近似根,如图8-1所示。
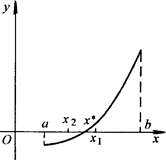
图8.1
不失一般性,假设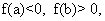 取 取
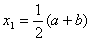
则必有下列三种情况之一成立:
(1)若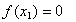 ,则 ,则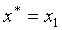 ; ;
(2)若 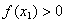 ,则 ,则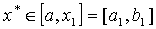 ; ;
(3) 若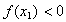 ,则 ,则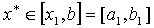 ; ;
无论那种情况,都将会得到
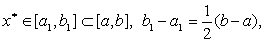
重复这一过程,假定已知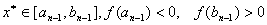 ,并取 ,并取
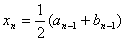
则必有下列三种情况之一成立:
(1)若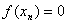 ,则 ,则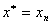 ; ;
(2)若 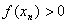 ,则 ,则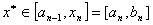 ; ;
(3) 若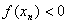 ,则 ,则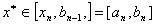 ; ;
无论那种情况,都将会得到
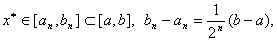
若再取
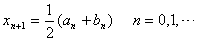 (8.1) (8.1)
作为所求根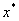 的近似值,式(8.1)为区间二分法的计算公式,其误差估计式为 的近似值,式(8.1)为区间二分法的计算公式,其误差估计式为
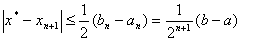 (8.2) (8.2)
综上所述,若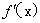 在区间 [a,b]上不变号,且 在区间 [a,b]上不变号,且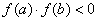 ,则由式(8.2)知 ,则由式(8.2)知
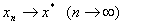
且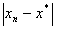 收敛于零的速度,相当于以 收敛于零的速度,相当于以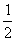 为公比的等比数列收敛于零的速度。 为公比的等比数列收敛于零的速度。
例1 用区间二分法求方程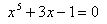 的最小正根。(准确到 的最小正根。(准确到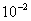 ) )
解:因为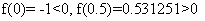 所以 所以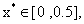 再由公式(8.2)求出 再由公式(8.2)求出
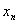 准确到 准确到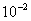 时,n的最小值, 令 时,n的最小值, 令
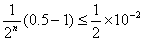
解得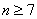 ,用区间二分法公式(8.1),具体计算结果列表如下: ,用区间二分法公式(8.1),具体计算结果列表如下:
表8-1
n |
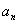
|
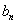
|
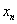
|
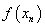
|
1 |
0 |
0. 5 |
0.25 |
- |
2 |
0.25 |
0.5 |
0.375 |
+ |
3 |
0.25 |
0.375 |
0.3125 |
- |
4 |
0.3125 |
0.375 |
0.34375 |
+ |
5 |
0.3125 |
0.34375 |
0.328125 |
- |
6 |
0.328125 |
0.34375 |
0.3359375 |
+ |
7 |
0.328125 |
0.3359375 |
0.33203125 |
 |
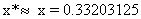
最后,我们指出区间二分法的优点是计算程序简单,只要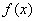 在区间[a,b]上连续,区间二分法就可使用,但区间二分法不能用来求偶次重根,由于区间二分法收敛比较慢,在实际计算中,区间二分法常用来求比较好的含根区间和初始近似值,以便进一步使用收敛更快的迭代法求出更精确的近似值。 在区间[a,b]上连续,区间二分法就可使用,但区间二分法不能用来求偶次重根,由于区间二分法收敛比较慢,在实际计算中,区间二分法常用来求比较好的含根区间和初始近似值,以便进一步使用收敛更快的迭代法求出更精确的近似值。
相关算法:求非线性方程实根的对分法
练习8.1
1.举例说明区间二分法不能求偶重根.
2.用区间二分法求方程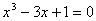 的最小正根,准确到 的最小正根,准确到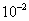 . .
练习题答案
1.提示:考虑方程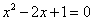
2.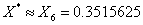
|
|