第1章 量子理论的实验基础
从17世纪到19世纪末，物理学迅速地发展起来，建立了完整的经典物理学体系（牛顿力学、电动力学、热力学和统计物理学）。它虽然成功地解释了许多物理现象，但仍然有许多现象，例如，黑体辐射、光电效应、康普顿效应、原子光谱、固体比热等实验是经典物理学无法解释的。面对这种成功与不足，虽有个别物理学家十分乐观，但更多物理学家忧虑忡忡。正如费曼所说:'人们经常听说19世纪后期的物理学家认为，他们已经了解所有有意义的物理规律，因而以后所能作的只是去计算更多的小数位。某个人可能这么说过一次，其他就争相传抄。但是彻底查阅当时的文献表明，他们所有的人都是对某些问题忧虑重重。'以后的发展表明，这些物理学家的忧虑是有道理的。实际上，正是这些实验导致了物理学新的革命，导致了量子力学的诞生。
§1.1 黑体辐射与普朗克的量子假设
1． 黑体辐射（动画演示）
19世纪末，钢铁工业迅速发展。为了保证钢铁的质量，必须确定铁水出炉时的温度。人们发现不同温度的铁水发出最强光的波长是不同的。另一方面，天文学为了确定恒星温度，也需要研究恒星发出最强光的波长与温度的关系。为了确定这一关系，需研究绝对黑体在一定温度下，在辐射平衡时，在频率范围
中绝对黑体辐射能量密度
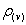与频率ν的关系。这些关系曲线如图1所示。这里所谓绝对黑体是指能吸收投射到它表面上各种波长全部辐射的物体，简称黑体。一个开有小孔的空腔或宇宙空间可视为黑体。这些ρ～ν曲线不能由经典物理推出。
青年物理学家维恩（Wien）1896年从热力学出发，再对黑体的发射和吸收过程作一些特殊的假设后，得到半经验公式为
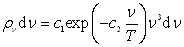（1.1.1）
式中，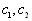
为常数。该公式在高频时与实验符合，在低频时与实验不符。
瑞利（Rayleigh，1900）和金斯（Jeans，1905）利用电动力学和经典统计理论导出了另一个黑体辐射公式
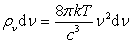（1.1.2）
式中，
是光速，
是玻耳兹曼（Boltzmann）常数。瑞利-金斯公式与维恩公式刚好相反，只在低频时与实验结果符合，而在高频时与实验结果不符。容易看出，在频率趋于无穷大时，辐射能量也将趋于无穷大。这显然不合理实际上，经典物理在这里遇到的困难是显然的。因为空腔壁是由有限原子分子组成的，自由度是有限的。而封闭在这种空腔里的电磁场是一个无限自由度的系统。由能量均分定理可看出，自由度分别为有限和无限的两系统不可能实现辐射热平衡。这是一个根本性的问题。