§1.4原子光谱及玻尔模型
由卢瑟福散射实验确定的原子模型是:在原子序数为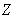 的元素的中心处,有一个正电荷为
的元素的中心处,有一个正电荷为
 的原子核,其半径
的原子核,其半径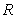 的数量级与核子数
的数量级与核子数 的三分之一次方成正比,即
的三分之一次方成正比,即
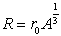
其中,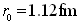 ,在正常情况下,核外有
,在正常情况下,核外有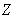 个电子环绕核旋转。
个电子环绕核旋转。
另一方面,实验发现,原子光谱是线状光谱。1885年,巴耳末(Balmer)给出了计算氢原子光谱的公式
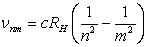 (1.3.1)
(1.3.1)
称之为巴耳末公式,其中, 称为里德伯(Rydberg)常数,
称为里德伯(Rydberg)常数,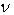 为频率,
为频率,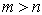 ,且
,且
 和
和 皆为整数。
皆为整数。
原子的线状光谱和原子的稳定性不可能由经典理论解释。按经典理论,在原子中作加速运动的电子必将产生辐射,其辐射频率应该是连续的,而非线状的;电子通过辐射放出能量后,会沿着螺旋线不断地落向原子核,最终会掉到到原子核上去,这样原子就不可能是稳定的。可是,事实并非如此。
为解释这些实验结果,1913年,年轻的丹麦物理学家玻尔(Bohr)提出了两个重要的假设:
1. 定态假设: 原子能且只能稳定地存在于与分立的能量相应的一系列状态中,这些状态称为定态。原子能量的任何变化,都只能在两个定态之间以跃迁的方式进行。
2. 跃迁假设: 原子在能量分别为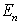 和
和 (
(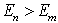 )的两个定态之间跃迁时,发射或吸收的电磁辐射的频率
)的两个定态之间跃迁时,发射或吸收的电磁辐射的频率
 满足如下的关系式
满足如下的关系式
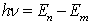 。 (1.3.2)
。 (1.3.2)
显然,仅这两个假设还不能解决全部问题。因为怎样确定定态的问题还未解决。玻尔根据他的对应原理(在大量子数的极限下,量子体系的行为趋近于经典体系的行为)得出角动量量子化条件,即,
3.作圆周运动的电子的角动量 只能是
只能是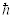 的整数倍,
的整数倍,
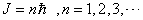 (1.3.3)
(1.3.3)
1916年,索末菲(Sommerfeld)将其推广到不限于圆轨道的周期过程和多自由度情况,
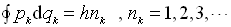 (1.3.4)
(1.3.4)
其中,
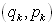 为一对共轭的正则坐标和正则动量,
为一对共轭的正则坐标和正则动量,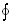 表示对一个周期运动的积分。(1.3.4)被称之为玻尔-索末菲量子化条件。
表示对一个周期运动的积分。(1.3.4)被称之为玻尔-索末菲量子化条件。
玻尔的量子论不但解释了实验上已发现的氢原子的光谱系,而且,预言的新譜系也被莱曼(Lyman)在实验中观测到,预言的
 光谱也被证实。玻尔理论也直接解决了原子稳定性问题,并且与普朗克-爱因斯坦的光量子假说相一致(原子定态的能级差和光量子的能量都是量子化的)。
光谱也被证实。玻尔理论也直接解决了原子稳定性问题,并且与普朗克-爱因斯坦的光量子假说相一致(原子定态的能级差和光量子的能量都是量子化的)。
玻尔量子论的局限性和存在的问题是,它无法解释复杂原子的光谱结构;不能给出处理譜线强度的方法;不能处理非束缚态的问题。