§1.5 德布洛意物质波假设与戴维逊-革末实验
§1.5.1 德布洛意物质波假设 (经典波实验动画演示)
按经典物理学，粒子和波是物质完全不同的两种存在形式。粒子具有确定的能量,动量,定域性和整体性。波具有干涉，衍射，叠加，非定域性和连续性。然而，由上面几个实验人们看到，电磁波作为一种波却具有粒子性，即具有波粒二象性。由此，由物质的统一性，人们自然去想，粒子是否也有波动性，即粒子也有波粒二象性呢？
1924年，德布洛意（de Broglie）在他的博士论文中对这个问题做了肯定的回答。
德布洛意假定：所有粒子都如同光子一样，既有粒子性，也有波动性。表征其粒子性的能量
，动量
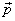和表征其波动性的频率
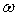，波矢量
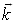的关系为（称之为德布洛意关系）
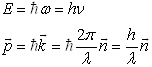。 （1.4.1）
与自由粒子相联系的波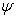 
称为物质波或德布洛意波，
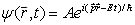， （1.4.2）
式中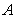 
是波振幅。
戴维逊（Davission）和革末（Germer）在1927年用实验直接证明了粒子的波动性（即波动特有的干涉和衍射现象）。他们用具有一定动量（从而具有一定波长）的电子垂直入射到磨光镍单晶的一个晶面上，测量不同角度的反射波强度。其结果与X-光在光栅上的衍射现象相似。在这里，磨光的镍单晶晶面等效于一个反射光栅。不同取向的晶面，光栅常数
不同。当电子波长
，
与角
（反射电子动量与晶面法线的夹角）满足
，
（1.4.3）
，反射波加强，电子密度极大。实验结果与理论预言完全一致。
此后的大量实验证实，中子，原子，分子等也都具有波动性。波动性是物质粒子的普遍属性。
粒子具有波动性与我们的经验似乎很难一致。这主要因为物质波的波长很短，而只有当这一波长不小于仪器的孔或屏的特征长度时，干涉和衍射现象才会出现，所以一般观察不到物质波的干涉和衍射现象。例如能量为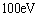
的自由电子的德布洛意波长
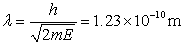， 这与原子大小相近。因此在一般的宏观条件下，其波动性不能表现出来。与光子类比是有益处的。17世纪牛顿提出光的微粒说。后来惠更斯提出光的波动说。但直到19世纪光的干涉衍射性被实验证实之后，光的波动说才被承认。到了20世纪，黑体辐射，光电效应，康普顿效应等实验证明了光既有波动性又有粒子性。可见，物资的本质只能根据物理实验确定，而不能仅凭经验去想象。与电磁波相似，粒子也是既有波动性又有粒子性。什么情况下粒子波动性才可忽略呢？粗略地说，当运动粒子的德布洛意波长远小于该粒子本身的尺度时，可忽略其波动性，近似地用经典理论来处理；否则，不可忽略其波动性，要用量子理论来处理。
应该指出，在电子的晶体衍射实验中，能够直接测量的仅是相应的波长，而不是频率。这与相应的光学实验一样。