第2章
函数与薛定谔方程
§2.1 波函数的统计诠释
§2.1.1
波粒两象性
1、经典物理学不可能对德布洛意给出正确解释
德布洛意的物质波假设的实质是：每一个粒子都必然地伴随一个德布洛意波，每一个粒子都既有粒子的性质，又有波动的性质，就是所谓的波粒两象性。那么粒子性和波动性是怎样联系的呢？须知，按经典物理学的概念，粒子性和波动性是相互排斥、完全不同的两种性质。粒子性就是一个物理实在的整体性、定域性，整体性即其整体地参与作用，定域性即其存在空间范围的有限性，例如一个质点，其运动自然在空间划出一条轨道，不弥散。而波动性是非整体性、非定域性，表现为连续、广延、弥散、干涉、衍射。一个统一体怎样同时具有这两种性质呢？
从经典物理学的概念出发，有一种观点认为：把电子看作为某种物质波形成的波包。这种观点的根据是波包的群速度
等于粒子的速度
。由德布洛意关系，在相对论的情况下，
；
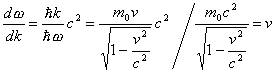在非相对论的情况下，
。
在两种情况下，都能得到粒子的速度就是波包的群速度。由此似乎可
将粒子看作波包，但这是行不通的。因为
，波包必然要弥散到很大的空间中去。这显然与粒子的有限大小完全不符。在迭加原理（见后）成立的线性理论中，不可能有孤立子解（不扩散且局限在空间小区域中的波包），以上分析无疑是正确的。实际上，在非线性理论中，既使孤立子解存在，也不能将粒子看作德布洛意波的波包。孤立子本质上不同于通常粒子。
另一种观点是，电子德布洛意波是由分布于空间中的大量电子形成的。这也是错误的。在戴维逊－革末实验中，如果让电子一个一个的入射，那么，开始时，底板上只有一个一个孤立的斑点，看不出任何规律，但长时间之后，底板上将出现很有规律的，与大量电子同时入射相同的干涉花样。这充分说明单个电子也有波动性，每个电子都有属于它自己的德布洛意波。氢原子只有一个电子，这一电子运动的稳定性和能级的量子化也充分说明了单个电子必然伴随有属于它自己的德布洛意波。
以上分析表明，在经典物理学基础上，很难解释清楚德布洛意波。电子不是经典物理学意义上的粒子，也不是经典物理学意义上的波。按经典物理学，所谓粒子，必具确定的电荷及质量；其运动状态由其确定的位置和动量描述，因而其运动必有确切的轨道；并且是整体性地参与相互作用。所谓波，其存在范围是非定域的，不是波动的各个部分同时参与作用，同时发生变化，而是其某一部分参与作用后，发生变化，再将作用逐渐传播开来；波动由其振幅，频率
和波矢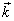 
描述，遵循相应的经典波动方程；对于线性波动方程，迭加原理成立，因而有干涉和衍射现象；量子理论中的粒子，即伴随着德布洛意波的粒子，不可能同时有确定的动量和位置，因而不可能再有确定的运动轨迹，这不同于经典粒子；
另一方面，可以同时有确定值的，能完全确定粒子状态的一组物理量，也完全确定了伴随粒子的德布洛意波的波包。粒子是整体地参与作用，因而其德布洛意波包也必然整体地参与作用，整体同时发生变化。例如，当处于氢原子基态的电子吸收了光子后跃迁到激发态时，与其伴随的波包也必然同时由基态波包变为激发态波包。
可见，粒子的整体性决定了伴随着它的德布洛意波包也具有整体性，即其整体地参与作用，整体同时发生变化。这是德布洛意波包的一个重要性质。这显然不同于经典波的性质。
由以上分析，我们看到，由于粒子伴随有德布洛意波，它失去了部分粒子性质（运动轨迹），仅保留有整体性这一性质；德布洛意波是一种波，但由于其伴随有粒子，它失去了部分波动性，仅保留了部分波动性（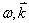
及迭加性）。