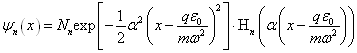（8）
由此可见，对于有的问题可以通过坐标变换直接得到其本征解，从而，避免求解复杂的本征方程。
例题3.5 在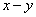 
平面上，质量分别为 
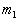和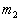 
的两个质点，用长度为 
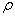的无质量的棒将其连接，构成所谓的刚性平面转子。求其能量本征值及其相应的波函数。
解：平面转子的定态薛定谔方程为
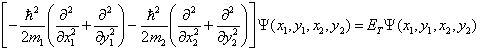（1）
令
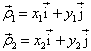（2）
引入质心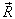坐标 
和相对坐标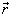 
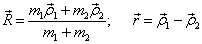（3）
质心质量
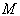与折合质量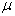 
分别为
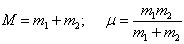（4）
方程（1）可以分离为质心运动与相对运动两个方程，即
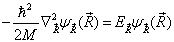（5）
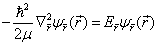（6）
若取质心运动的能量为能量零点，则只需求解平面转子相对运动满足的本征方程（6）式即可。由于相对坐标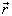 
的长度不变，故有
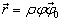（7）
于是，（6）式可以改写成