伽莫夫(Gamow)利用波动力学的这一效应很好地说明了放射性元素的 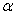 衰变现象。此外,诸如金属电子的冷发射、半导体
衰变现象。此外,诸如金属电子的冷发射、半导体 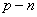 结、遂道二极管也都是这一效应的表现。
结、遂道二极管也都是这一效应的表现。
当
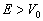 时,
时,
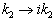 。
。
将(3.5.9)中的![]() 用
用![]() 代替就得到这种情况下的透射系数和反射系数,
代替就得到这种情况下的透射系数和反射系数,
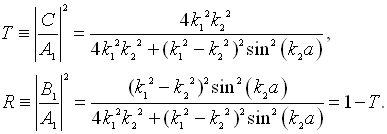 (3.5.12)
(3.5.12)
式中
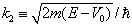 。
。
由上式可以看出,虽然
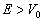 ,粒子总会以确定的几率被反射回来。这也是粒子波动性的表现。特别是当
,粒子总会以确定的几率被反射回来。这也是粒子波动性的表现。特别是当![]() 时,
时,![]() ,称为共振透射。
,称为共振透射。
将(3.5.10)式中 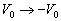 ,则可得到粒子入射到势阱时的透射系数和反射系数。这时
,则可得到粒子入射到势阱时的透射系数和反射系数。这时
![]() 。
。
当
![]() ,
,![]() ,
,
这时的共振能量是
![]() 。
。
其物理意义是,粒子在势阱中碰到两壁时,必发生透射与反射。实际上透射出去的波幅是初次透射波和经各次反射(在![]() )后再透射出去的波的波幅之和。当满足上面条件时,这些透射出去的波的位相相同,彼此相干叠加,从而出现共振透射。
如图3.5所示
)后再透射出去的波的波幅之和。当满足上面条件时,这些透射出去的波的位相相同,彼此相干叠加,从而出现共振透射。
如图3.5所示
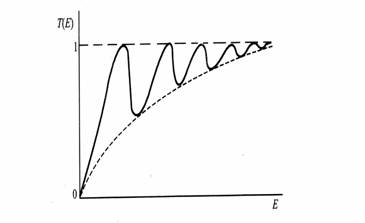
图 3.5 共振透射
如取极限
![]() ,
,
但
![]() ,
,
就能利用(3.5.9)
或(3.5.10)讨论![]() 势垒的反射与透射,但没有直接求解更方便。
势垒的反射与透射,但没有直接求解更方便。