故宇称守恒,且 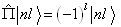 。这里
。这里 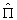 为空间反演算符,因此
为空间反演算符,因此
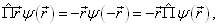
因为 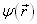 任意,所以
任意,所以
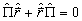 ,即
,即
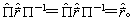
这样![]()
![]()
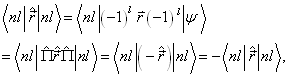
因此,
 。
。
同理,由于 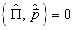 ,
, 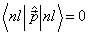 。
。
例题4.14设 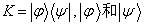 是两个任意矢量,均已归一化,问
是两个任意矢量,均已归一化,问
( 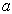 )在什么条件下,
)在什么条件下, 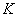 是厄米算符?
是厄米算符?
( 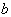 )在什么条件下,
)在什么条件下, 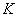 是投影算符?
是投影算符?
解:(
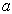 )先证明
)先证明
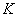 的厄米共轭为
的厄米共轭为
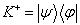 。设
。设
 和
和
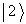 为两任意态矢量,
为两任意态矢量,
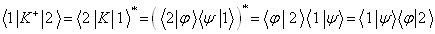
因
 和
和
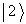 为任意矢量,所以
为任意矢量,所以
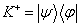 (1)
(1)
再讨论
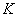 是厄米算符的条件。若
是厄米算符的条件。若
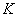 是厄米算符,须满足
是厄米算符,须满足
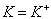 ,
,
即
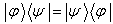 (2)
(2)
两边作用到 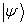 上,有
上,有
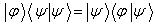
即
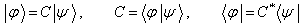 (3)
(3)
代入式(2),得
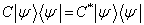
即
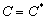 (4)
(4)
所以
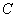 为实数。因此,只有在
为实数。因此,只有在

为实数时,
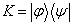 才是厄米算符。
才是厄米算符。
( 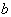 )投影算符的充要条件是
)投影算符的充要条件是
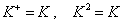 。由(
。由( 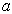 )中讨论的结论,知
)中讨论的结论,知 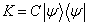 (
( 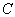 为实)已是厄米算符,故只要将它代入
为实)已是厄米算符,故只要将它代入 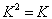 ,定出实常数
,定出实常数
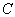 就能求出
就能求出
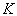 是投影算符的条件,
即
是投影算符的条件,
即
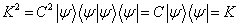
亦即
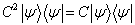
亦即

从而
 (这里不取
(这里不取 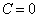 )
)
所以当
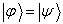 时,
时,
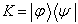 才是投影算符。
才是投影算符。
例题4.15设属于能级
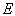 有三个简并态
有三个简并态
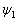 ,
,
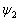 和
和  ,彼此线形独立,但不正交,试利用它们构成一组彼此正交归一的波函数。
,彼此线形独立,但不正交,试利用它们构成一组彼此正交归一的波函数。
解:
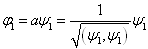
 ,
, 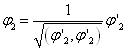 ,
,
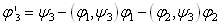 ,
,
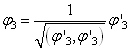 。
。
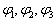 是归一化的。
是归一化的。
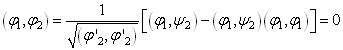 ,
,
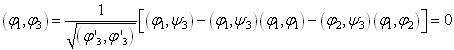 ,
,
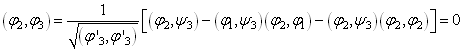
![]() 它们是正交归一的,但仍然是简并的(可验证:它们仍对应于同一能级)。
它们是正交归一的,但仍然是简并的(可验证:它们仍对应于同一能级)。
例题4.16设
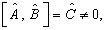
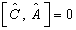 ,
, 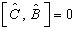 ,
,
试计算
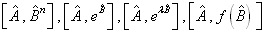 ,
,
证明Glauber公式:
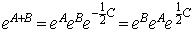
解
1.由前提可知, 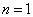 ,
, 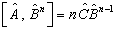 成立。设
成立。设 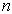 为任意正整数时
为任意正整数时
 ,
,
则
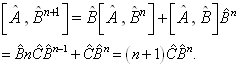 (1)
(1)
2.
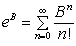
∴
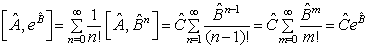 (2)
(2)
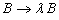 ,则
,则 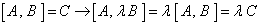 ,式(4)作此置换,
,式(4)作此置换,