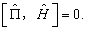当粒子处于状态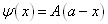
时，首先，利用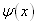 
的归一化条件求出归一化常数的模方为
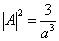（10）
其次，将波函数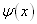 
向能量的本征函数系作展开，得到展开系数
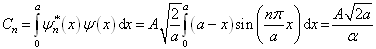（11）
进而有
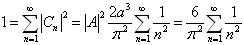（12）
于是得到无穷级数之和
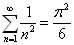（13）
进而得到另外两个无穷级数之和
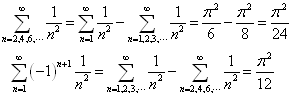（14）
例题4.11
试确定一维坐标与动量本征态的坐标与动量均方根误差。
解：假设作一维自由运动的粒子具有确定的动量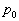 
，相应的本征波函数为平面波
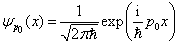(1)
它的坐标几率密度
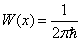(2)
这就意味着，当该粒子的动量确定时，由于坐标几率密度与坐标变量无关，故粒子出现在空间任何一点的几率都是相同的，也就是说粒子的坐标完全是不确定的，即
；
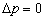(3)
其次，假设粒子具有确定的坐标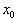 
，相应的本征波函数为
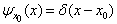（4)
将其向动量的本征函数作展开，
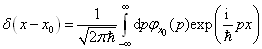(5
其展开系数为
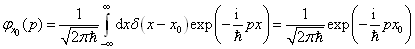(6)
展开系数的模方就是动量的取值几率密度，即
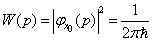(7)
这意味着，当该粒子的坐标确定时，由于动量几率密度与动量无关，故具有任何动量值的几率密度都是相同的，也就是说粒子的动量完全是不确定的，它们的均方根误差分别为
；
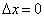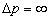(8)
可见，当粒子的动量确定时，它的坐标完全不能确定；当粒子的坐标确定时，它的动量完全不能确定。
例题4.12如果
， 
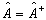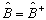且 
，
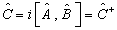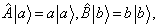
都是束缚态，则
证明：
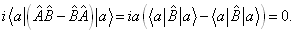
这里考虑了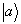 
是束缚态，因而 
是有限的，及 
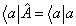。同理可证
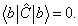
如令
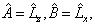
则
，
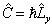由此得
。
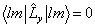例题4.13粒子在位势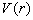 
的有心力场中作定态运动，且
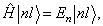
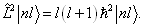
求证：
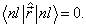
证明：有心力场中，由于总哈密顿算符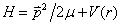 
具有空间反射不变性，即
