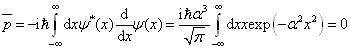 (5)
(5)
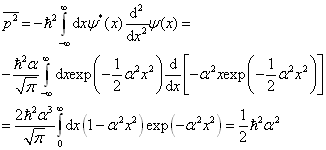 (6)
(6)
将其代入(1)式,得到
 (7)
(7)
计算中应注意技巧。例如,(2)式为零是因为被积函数是奇函数;(5)式为零是因为右边为实,左边纯虚。
例题4.9
设体系的哈密顿算符为
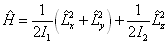
求其能量本征值。
解:将哈密顿算符改写为
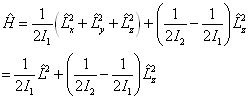 (1)
(1)
显然, 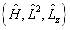 构成力学量完全集,且其共同本征函数系为
构成力学量完全集,且其共同本征函数系为 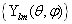 ,于是
,于是
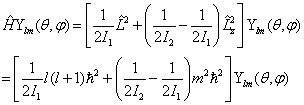 (2)
(2)
进而可知能量本征值为
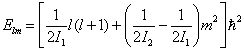 (3)
(3)
例题4.10
粒子在宽度为 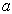 的非对称一维无限深势阱中运动,若粒子分别处于状态
的非对称一维无限深势阱中运动,若粒子分别处于状态
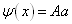 ;
;
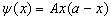
式中 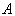 为归一化常数。证明如下无穷级数之求和公式
为归一化常数。证明如下无穷级数之求和公式
; 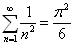 ;
;
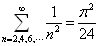
解:在宽度为
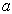 的非对称一维无限深势阱中运动的粒子,其能量本征值与本征函数分别为
的非对称一维无限深势阱中运动的粒子,其能量本征值与本征函数分别为
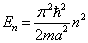 ,
,
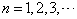 (1)
(1)
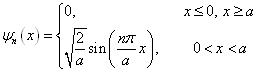 (2)
(2)
当粒子处于状态 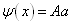 时,首先,利用
时,首先,利用 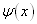 的归一化条件求出归一化常数
的归一化条件求出归一化常数 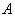 ,即
,即
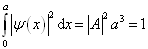 (3)
(3)
于是,得到归一化常数的模方为
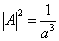 (4)
(4)
其次,将波函数 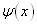 向能量的本征函数系作展开,得到
向能量的本征函数系作展开,得到
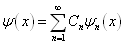 (5)
(5)
式中的展开系数为
 (6)
(6)
式中, 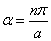 。显然,当
。显然,当 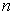 为偶数时,
为偶数时, 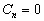 ,而当
,而当
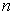 为奇数时,
为奇数时,
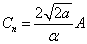 (7)
(7)
由展开系数的模方之和为1可知
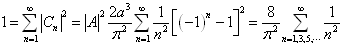 (8)
(8)
于是,得到无穷级数之和
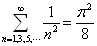 (9)
(9)