§6.4.3 球谐振子与氢原子之间的关系
从表面上看，氢原子与球谐振子是两个完全不同的物理问题，但是，有一点是相同的，那就是它们都处于中心力场之中。通过下面的推导可以由氢原子的解得到球谐振子的解。
球谐振子的位势
(6.4.26)
式中，
(6.4.27)
其本征波函数为
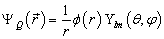
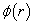满足的径向方程为
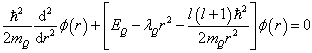(6.4.29)
氢原子的位势为库仑场
(6.4.30)
式中，
其本征波函数为
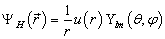(6.4.32)
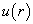满足的径向方程为
(6.4.29)式与(6.4.33)式的差别仅在于位势的不同，若对(6.4.29)式作如下的变换
，
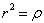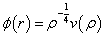(6.4.34)
则可得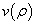 
满足的方程
(6.4.35)
式中，
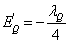(6.4.36)
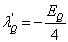(6.4.37)
(6.4.38)
由(6.5.38)式可以解得
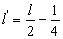(6.4.39)
比较发现，(6.4.33)式与(6.4.35)式在形式上是完全相同的两个微分方程，两者的变量之间满足如下对应关系：
； 
； 
； 
；
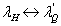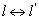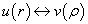(6.4.40)
已知氢原子的能量本征值为
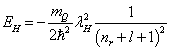(6.4.41)
利用(6.4.40)式的对应关系可知
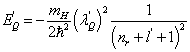(6.4.42)
再将(6.4.36)、(6.4.37)及(6.4.39)式代入上式，整理后得到
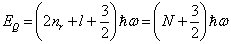(6.4.43)
此即球谐振子的能量本征值。