例题6.2
质量为  的粒子处于中心力场
的粒子处于中心力场
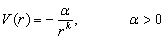
证明存在束缚态的条件是 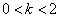 。
。
证明:由维里定理知,在定态之下,当势能可以写成坐标的齐次函数时,
 (1)
(1)
这里,
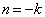 (2)
(2)
故有
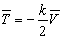 (3)
(3)
而总能量
 (4)
(4)
由于,动能的平均值大于零,束缚态的总能量小于零,所以,要求
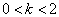 。
。
例题6.3 定义径向动量算符

试导出其球坐标系中的表达式,进而求出 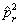 及
及 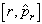 。
。
解:设 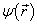 为体系的任意一个状态,由径向动量算符的定义可知
为体系的任意一个状态,由径向动量算符的定义可知
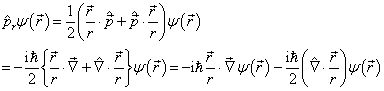 (1)
(1)
利用
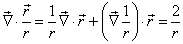 (2)
(2)
再顾及到球坐标系中动量算符的形式
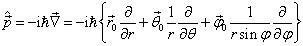 (3)
(3)
(1)式可写为
 (4)
(4)
由 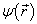 的任意性可知
的任意性可知
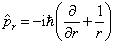 (5)
(5)
由上式容易求出
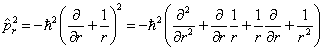 (6)
(6)
将其作用到一个任意的状态
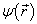 上,有
上,有
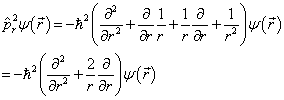 (7)
(7)
由
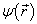 的任意性可知
的任意性可知
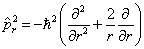 (8)
(8)
将对易关系  作用到任意一个状态
作用到任意一个状态
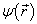 上,即
上,即
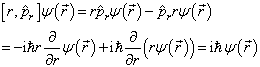 (9)
(9)
于是,得到与直角坐标系相同的对易关系
 (10)
(10)
例题6.4
为简化,常用原子单位,即在库仑势及薛定锷方程中令  。在最后结果中,再根据量纲,代入
。在最后结果中,再根据量纲,代入 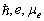 的适当组合。试由
的适当组合。试由
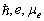 给出质量,长度,时间,速度,动量,能量。
给出质量,长度,时间,速度,动量,能量。
 ;长度:乘以
;长度:乘以 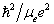 ;时间:乘以
;时间:乘以  ;速度:乘以
;速度:乘以  ;动量:
;动量:
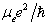 ;能量:
;能量:  。
。