§6.2.3
讨论
1、类氢离子
一个电子与带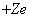 
电荷的原子核构成的体系为类氢离子。上述推导过程对类氢离子也是适用的，只不过公式中的 
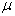表示相应的约化质量，并且，在与电荷平方 
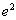相关处再乘上正电荷数 
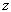而已，即
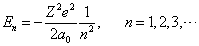(6.2.50)
(6.2.51)
(6.2.52)
与角度相关的球谐函数没有变化。
2、能谱
由能量本征值的表达式可以看出，束缚态的能量是负的，基态能量为 
。随着量子数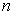 
的增大其绝对值变小，当
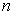非常大时，能级会变得特别密集，并接近于零。
对于氢原子，若令
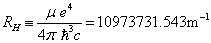(6.2.53)
则其能量本征值公式可以改写为
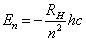(6.2.54)
它与玻尔的量子论给出的结果是完全一致的。
对于中心力场而言，简并度为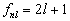 
，而氢原子的能级只与量子数
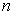有关，故其简并度
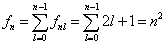(6.2.55)
说明库仑场带来的简并度高于一般的中心力场。
3、坐标的几率分布
求出了定态波函数，就等于知道了电子坐标的几率分布
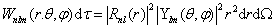(6.2.56)
径向几率分布。
将上式对角度部分作积分，有
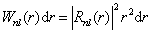(6.2.57)
径向几率密度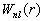 
表示在半径为 
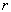的单位厚度的球壳中发现一个电子的几率。如图6.2所示
图6.2 氢原子中电子径向分布（取自曾谨言《量子力学教程》）。
对基态而言，有
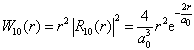(6.2.58)
那么，电子出现在什么地方的几率最大呢？只要将上式对变量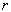 
求导并使之等于零，即
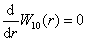(6.2.59)
于是，有
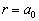(6.2.60)
说明在基态下电子最可能出现在径向长度等于玻尔半径的地方。
几率的角度分布。
将(6.2.56)式对径向部分作积分，有
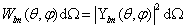(6.2.61)
从上式知道几率的角度分布与主量子数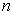 
无关，并且，与角度 
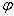也无关，即
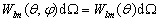(6.2.62)
说明几率的角分布是关于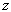 
轴旋转对称的。另外，利用
(6.2.63)
可知，
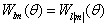(6.2.64)