而 
指数
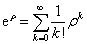(6.2.29)
当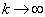 
时，它的展开形式的渐近行为也是
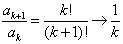(6.2.30)
这说明它的渐近行为与函数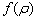 
是完全一样的。于是，有
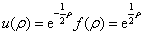(6.2.31)
但是，上式与波函数的有限性相矛盾。
为了满足波函数的有限性要求，必须对无穷级数作截断。设最高次项为 
，即要求
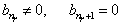(6.2.32)
由(6.3.27)式可知，满足上述要求的
为
(6.2.33)
于是，可以得到能量量子化的条件
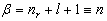(6.2.34)
其中，各量子数的取值范围是
为了得到能量本征值的具体表达式，利用(6.2.34)、(6.2.17)与(6.2.19)式，进行简单的代数运算，得到
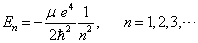(6.2.35)
此即氢原子束缚态的能量本征值表达式。
将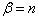 
及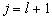 
代入(6.2.27)式，整理后得到
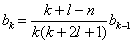(6.2.36)
于是，有
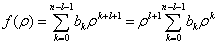(6.2.37)
利用递推公式(6.2.36)可知
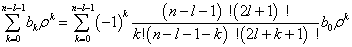(6.2.38)
而连带拉盖尔（Laguerre）多项式为
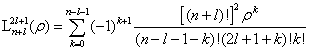(6.2.39)
故有
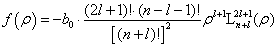(6.2.40)
再将其代入径向波函数，得到
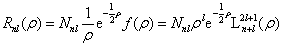(6.2.41)
而
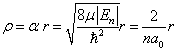(6.2.42)
其中，
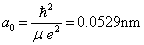(6.2.43)
称为玻尔半径。将(6.2.42)式代入(6.2.41)式，有
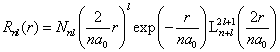(6.2.44)
式中的归一化常数 
可以由归一化条件
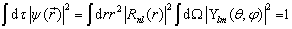(6.2.45)
确定为
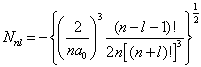(6.2.46)
综上所述，氢原子的能量本征值和相应的本征波函数为
(6.2.47)
(6.2.48)
为了使用方便，下面列出氢原子的前几个波函数：
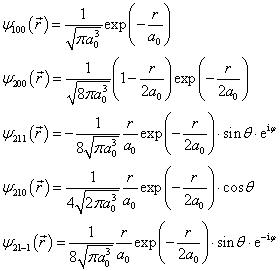(6.2.49)