§6进一步学习的内容
§6.3无限深球方势阱
设
(6.3.1)
称这一中心力场为无限深球方势阱。在其中运动的、质量为 
的粒子满足的径向方程为
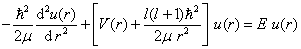(6.3.2)
当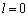 
时，径向方程简化为
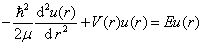(6.3.3)
在势阱外（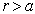 
），由于位势是无穷大，
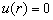(6.3.4)
方程(6.3.3)及边界条件(6.3.4)与一维无限深势阱相同，所以其解及能级也必相同，即
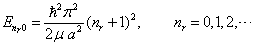(6.3.5)
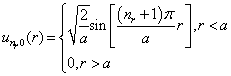(6.3.6)
当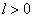 
时， 
，仍有 
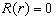。当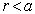 
，(6.3.2)可改写为
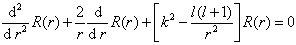(6.3.7)
式中，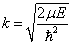 
。令
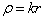(6.3.8)
则(6.3.7)式化为
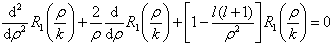(6.3. 9)
此即球贝塞耳(Bessel)方程。它的解是球贝塞耳函数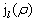 
和球诺依曼（Neumann）函数 
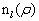。在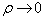 
时，它们的渐近行为分别为
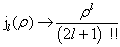(6.3.10)
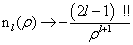(6.3.11)
显然，在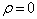 
处，球诺依曼函数不满足波函数的有限性要求，所以，在球方势阱的内区，
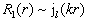(6.3.12)
利用边界条件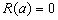 
，得到能量本征值满足的超越方程为
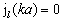(6.3.13)
当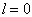 
时，能重新得到(6.3.5)－(6.3.6)。
当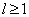 
时，能量本征值满足的方程是一个超越方程，所以必须进行数值求解或者用作图法求解。