§6.4球谐振子
在笛卡儿坐标系中，利用分立变量法，容易得到三维各向同性谐振子
的解。这里在球坐标系中求解，主要是训练解题方法.
质量为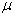 
角频率为 
的球谐振子的势能为
(6.4.1)
其径向方程可以写成
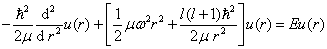(6.4.2)
令
； 
；
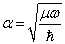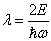(6.4.3)
则可以将(6.4.2)式改写成
(6.4.4)
上述方程有两个奇点：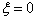 
和 
。
当 
时，上式变成
(6.4.5)
可以其渐近解是
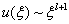(6.5.6)
当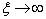 
时，(6.4.4)式变为
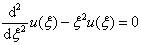(6.5.7)
满足波函数自然条件的解为
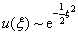(6.4.8)
于是，(6.4.4)式解的一般形式可取为
(6.4.9)
其中，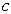 
为一个复常数。
将(6.4.9)式代入方程(6.4.4)，得到
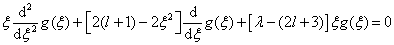(6.4.10)
令
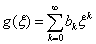(6.4.11)
并将其代入(6.4.10)式，得
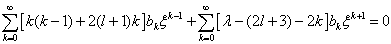(6.4.12)