§
7。1 自旋存在的实验基础
最直接地证实存在自旋的实验是史特恩—盖拉赫（Stern-Ger-lach）实验，而光谱的精细结构和反常塞曼效应间接地证实了自旋的存在。
1．
史特恩—盖拉赫实验
实验装置示意图如图1所示。在真空之中，电炉K加热后放出氢原子蒸汽，经狭缝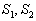 
后，成为x方向的水平原子束，让它通过不均匀磁场NS。在它前进的方向上置一照相版pp，原子打在其上可留下斑点。
图7.1
史特恩—盖拉赫实验
这个实验的关键在于磁场的不均匀性，因为带磁矩的粒子只在非均匀磁场中才受力的作用，而“不均匀性”是相对而言的，实验的对象是原子束，因此这种不均匀性应该在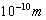 
的线度内呈现出来（请考虑，如果用线度小于 
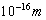的电子代替原子来作实验，将会怎样？）。
其次，在这个实验中原子束的氢原子处于基态。在电炉K中加热样品，当达到热平衡时，原子的动能为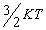 
；当 
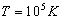时，动能大约为8—9eV。这能量值小于氢原子的第一激发态能
。通常加热的温度远小于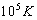 
，因此从源中出来的氢原子总是处于基态，其磁矩为零。因此，如果这样的原子受到了磁场的作用，其磁矩必有另外的起因。
设非均匀磁场沿z轴方向，磁场长度为d，磁矩为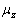 
的中性原子进入磁场后在力 
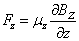的作用下，原子在磁场区内做抛物线运动：
水平方向： 
（ 
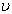为原子入射速度）
z方向：
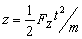
到磁场区的出口处，所用时间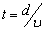 
。因此在出口处，原子偏离x轴的距离为a，偏转角为 
：
。
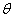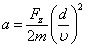
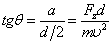（7.1）
从而原子束离开磁场后沿直线方向打向pp，垂直距离为b：
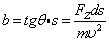
将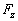 
的值代入得
入射原子的动能为
，
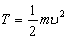设
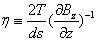
则在z方向的磁矩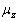 
为
。
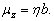（7.2）
b的取值可以由实验测出，而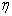 
完全由实验装置和原子动能决定。因此通过史特恩—盖拉赫实验，可以直接给出
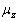的取值情况。
在1921年和1927年分别用银原子和氢原子成功地作了实验，原子束在pp上集结的痕迹刚好只有两个，而且它们的位置十分对称，强度也相同。这一情况清楚表明：原子具有磁矩（本征磁矩）。这本征磁矩在z方向上只取两个值，大小相等，方向相反。实验证实，电子本征磁矩的值是一个波尔磁子。
2．.光谱线的精细结构
观察Na光谱的主线系（np
3s）。由3p到3s发出一条谱线—D（黄）线。如果用高分辨率的摄谱仪或分光镜观察Na光谱由3p到3s发出的谱线——D（黄）线就会发现，D线实际上不是一条谱线，而是靠得十分近的两条谱线，波长分别为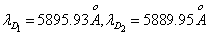 
，二者仅相差 
。
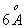这种现象表明光谱线具有精细结构。如果认为电子具有内禀磁矩的话，这一现象就容易解释。电子内禀磁矩在有轨道磁矩引起的“内磁场”的作用下，将使价电子受到力的作用，从而引起了附加能量。由于内禀磁矩的分量只有两个值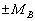 
，因此由此引起的附加能量 
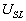也只有两个值，从而一条能级将分裂成两条。由于s能级无轨道磁矩，不存在内磁场，从而附加能量为零，如此s能级不分裂。但p能级将分裂成距离很近的两条 
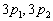。因此3p向3s跃迁时发出的谱线有两条。又因为 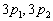相距很近，因此这两条谱线波长相差很小。精细结构是一切原子的特点，只不过碱金属原子的精细结构最为简单，最易于暴露内禀角动量的本质特点而已。
3．
反常赛曼效应
弱磁场中的反常赛曼效应（在弱磁场中原子光谱分裂为偶数条的复杂现象）也说明了电子必有内禀磁矩，从而有内禀角动量。