§7.2 电子自旋假设，自旋算符及自旋波函数
.电子自旋假设
1925年乌仑贝克和古兹米特提出，稍后由泡利加以完善的关于基本粒子存在自旋的假设如下:
（1）一切微观粒子都存在即内禀角动量，又称自旋。它是微观粒子的固有属性之一。自旋物理量用线性厄米算符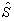 
描述。它具有与轨道角动量 
相同的性质。
（2）电子自旋在任意方向上的投影值都仅有两个，即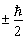 
，相应的磁矩为 
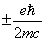，即回转磁比值 
。
这样，一个电子的自由度应为4，即除了空间自由度x,y,z外，还有一个与自旋相联系的自由度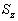 
，其本征值的特点是分立的，仅有二个值。
自旋算符
满足对易关系
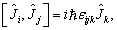
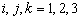，的算符称为角动量算符。自旋既然也是角动量，因此也必须满足角动量的对易关系。即，
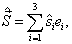
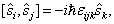
。 （7.2.1）
由于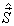 
在任一方向的投影只能是 
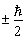，任意选定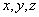 
坐标系后，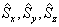 
的本征值都是 ； 
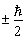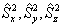的本征值都是 
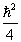。即，
（7.2.2）
由此得
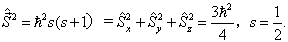（7.2.3）
由于
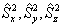的本征值只有一个，所以在任何表象中，
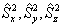都是单位矩阵乘以
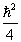。将第2式用分量写出，
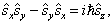（7.2.4a）
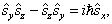（7.2.4b）
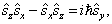（7.2.4c）
由（7.2.4），利用（7.2.2）可得
.
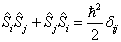（7.2.5）
由于 
， 
有共同的完备本征函数系。下面求在 表象中，
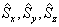的矩阵形式。由于 
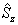只有两个本征值
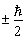，且在自身中表象，所以
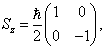（7.2.6）
设
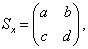
由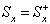 
及（7.2.5）可得，
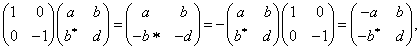
由此得
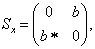
再考虑到
，
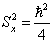可得
取 
，得到
（7.2.7）
将（7.2.6）及（7.2.7）代入（7.2.4c），可得
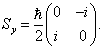（7.2.8）
由（7.2.6）－（7.2.8）可得
（7.2.9）
自旋波函数
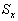的本征方程是
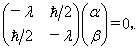（7.2.10）
由
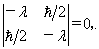
得 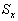的本征值是
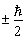。考虑到归一化后，得到 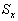的本征函数是
，
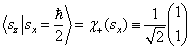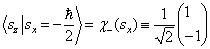。 （7.2.11）