§7.6
粒子全同性原理
1.
全同粒子
一位古代哲学家说过:‘一个人不能两次踏入同一条河流。’对于经典物理学,这无疑是对的。但对于量子力学,这显然就不再是正确的。例如所有电子的电荷都是同一的,所有处于基态的氢原子的性质也都完全一样。实际上,自然界既有本质上的连续性,又有本质上的离散性;既有任意大小的差别,又有绝对的同一。一切相反的两极都如同一张纸的正面和反面必然地相互依存着。唯如此,才能形成这丰富多彩的世界。这就是对立统一规律的本质。
由于量子理论,粒子的内禀属性才能有本质上的差别。例如自旋,只是由于相对论量子力学,才能推导出粒子自旋是整数或半整数,并由此将粒子分类为玻色子和费米子,它们分别满足玻色统计和费米统计。类似的,宇称、质量、也可以由量子场论算出,就是粒子电荷及电荷的量子化,以后也将由理论推导出。可见,只是由于量子力学,粒子的内禀属性(如电荷、静质量、自旋、宇称等)才是分立的,由此粒子才能分成许多种类。量子力学定义内禀属性完全相同的粒子为全同粒子。按经典力学,粒子的自旋可取任意值,例如 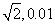 。因此按经典力学就不可能定义全同粒子。
。因此按经典力学就不可能定义全同粒子。
2.
粒子全同性原理
两个经典例子即使被看作全同的,它们仍然是可分辨的。因为它们有不同的、可分辨的运动轨迹。与此不同,量子力学的粒子伴随有德布罗意波,当两个全同粒子的德布罗意波重叠时,这两个全同粒子就不再是可以分辨的了。另一方面,既然两个粒子是全同的,它们交换时就不可能引起体系的任何变化。这就是说,两个全同粒子交换后,体系的哈密顿不变,体系的状态不变。这就是粒子全同性原理,或说量子体系具有全同粒子交换对称性。将这一原理用数学表达出来就是
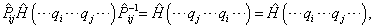
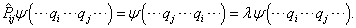
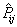 是粒子交换算符,
是粒子交换算符,  表示粒子的全部自由度(坐标与自旋)。(7.6.1)表明,全同粒子体系哈密顿具有全同粒子交换不变性;(7.6.2)表明,全同粒子体系不仅要满足薛定锷方程,而且要满足交换算符的本征方程。
表示粒子的全部自由度(坐标与自旋)。(7.6.1)表明,全同粒子体系哈密顿具有全同粒子交换不变性;(7.6.2)表明,全同粒子体系不仅要满足薛定锷方程,而且要满足交换算符的本征方程。
3.
全同粒子体系的波函数
显然
 由此
由此

实验表明,多个全同玻色子体系态函数是
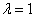 的本征态;多个全同费米子体系态函数是
的本征态;多个全同费米子体系态函数是 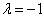 的本征态。如果两个费米子(第
的本征态。如果两个费米子(第 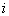 和第
和第 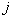 个)处于同一个态,则有
个)处于同一个态,则有
 (7.6.4)
(7.6.4)
另一方面,
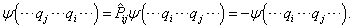
由(7.6.4)-(7.6.5)得
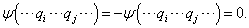 (7.6.6)
(7.6.6)
这说明费米子体系一个态上不能有两个或两个以上费米子,这正是泡利原理。可见,由全同性原理可以推导出泡利原理。类似的推导可以证明,玻色子体系同一个态上可有任意多个粒子。由此爱因斯坦预言了低温玻色子凝聚效应。这一效应已完全被现代实验所证实。
由(7.6.1)可知,

因此,全同粒子体系交换算符本征值是守恒量。
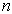 个全同粒子体系有
个全同粒子体系有 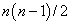 个交换算符,这些交换算符互不对易。例如,
个交换算符,这些交换算符互不对易。例如, 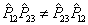 。不相互对易的算符可能有也可能没有共同本征态。
。不相互对易的算符可能有也可能没有共同本征态。
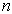 个全同粒子体系的
个全同粒子体系的 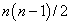 个交换算符恰好有共同本征态,那就是
个交换算符恰好有共同本征态,那就是 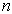 个全同粒子的全对称态函数和全反对称态函数。并且,可以证明,
个全同粒子的全对称态函数和全反对称态函数。并且,可以证明, 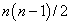 个交换算符的本征值都是相同的,即,都是1或都是
个交换算符的本征值都是相同的,即,都是1或都是 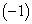 。
。 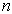 个全同玻色子体系应由全对称态函数描述,
个全同玻色子体系应由全对称态函数描述, 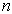 个全同费米子体系应由全反对称态函数描述。
个全同费米子体系应由全反对称态函数描述。
无相互作用的
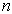 个全同粒子体系的哈密顿是
个全同粒子体系的哈密顿是
 (7.6.7)
(7.6.7)
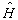 的本征值和本征函数显然是
的本征值和本征函数显然是
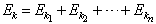 (7.6.8)
(7.6.8)
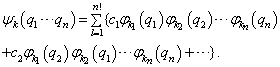 (7.6.9)
(7.6.9)
下脚标  表示粒子所处的单粒子态,大括弧内是
表示粒子所处的单粒子态,大括弧内是
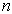 个粒子自由度一切可能交换的线性组合。
个粒子自由度一切可能交换的线性组合。
 是厄米算符,所以
是厄米算符,所以 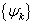 是完备本征函数系。因此,
是完备本征函数系。因此, 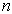 个全同粒子有相互作用的哈密顿
个全同粒子有相互作用的哈密顿  的本征函数
的本征函数 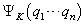 可用
可用 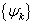 展开。如果
展开。如果 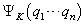 关于
关于 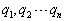 是对称或反对称的,则
是对称或反对称的,则 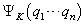 也是关于
也是关于 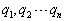 是对称或反对称的。可见,只要构造出对称或反对称的
是对称或反对称的。可见,只要构造出对称或反对称的 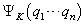 即可。
即可。
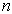 个无相互作用的全同费米子体系的态函数
个无相互作用的全同费米子体系的态函数
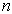 个无相互作用的全同费米子体系必然处于
个无相互作用的全同费米子体系必然处于 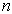 个不同的单粒子态上。相应的全反对成态函数是
个不同的单粒子态上。相应的全反对成态函数是
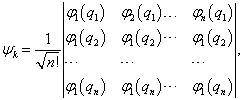 (7.6.10)
(7.6.10)
两个粒子交换相当于两行交换,两行交换时 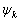 变号,因此满足全同费米子体系反对称的要求。
变号,因此满足全同费米子体系反对称的要求。