 个无相互作用的全同玻色子体系的波函数
个无相互作用的全同玻色子体系的波函数
设有 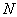 个全同玻色子,分布于
个全同玻色子,分布于  单粒子态
单粒子态 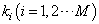 上。
上。  个玻色子处于
个玻色子处于  态上,
态上, 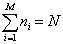 。因为可以有任意数目的玻色子处于相同的单粒子态,
。因为可以有任意数目的玻色子处于相同的单粒子态,
![]() 可以为0,可以为1,大于1,或等于
可以为0,可以为1,大于1,或等于 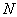 。此时,处于同一态上的玻色子自动是对称的。因此只要将不同态上的粒子对称化就可以了。这样,
。此时,处于同一态上的玻色子自动是对称的。因此只要将不同态上的粒子对称化就可以了。这样,  个全同玻色子的态函数就可表示为
个全同玻色子的态函数就可表示为
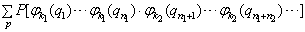 (7.6.11)
(7.6.11)
这里的P表示只对处于不同单粒子态上的粒子进行对换,这样得到的求和式中的各加项必正交且归一(设 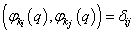 )。例如,
)。例如,
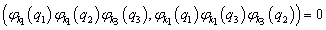 。
。
在同一个态的  个粒子相互对换,这一项不变。例如,
个粒子相互对换,这一项不变。例如,
 。
。
这种置换共有 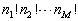 。由此,通过不同态中粒子置换得到的求和中的项数就是
。由此,通过不同态中粒子置换得到的求和中的项数就是
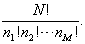 (7.6.12)
(7.6.12)
个。如此,归一化的对称波函数可表为
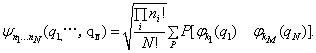 (7.6.13)
(7.6.13)
例如
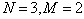
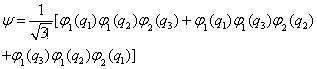
描述全同粒子体系的量子态的更简洁的形式是所谓二次量子化方法。这将在‘高量’中讨论。
4.全同粒子体系可能状态的数目
设有 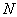 个全同粒子分布在
个全同粒子分布在 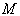 个可能的单粒子态上。显然,有多少分布方式就有多少种状态。
个可能的单粒子态上。显然,有多少分布方式就有多少种状态。
对于费米子,显然  是必须的。这时体系有
是必须的。这时体系有 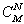 个可能状态。
个可能状态。
对于玻色子,可由以下考虑得到。将可能的单粒子态看作篮子,而玻色子看作全同的球。将左边第一个位置放一个篮子(任一个),将其余 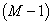 个篮子及
个篮子及 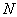 个球完全任意地在其右边排成一排。这种排列数是
个球完全任意地在其右边排成一排。这种排列数是 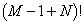 。这些排列方式中有许多是重复排列。其中
。这些排列方式中有许多是重复排列。其中 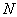 个球任意重新排列不改变排列方式,这种排列有
个球任意重新排列不改变排列方式,这种排列有  种;
种; 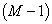 个篮子任意重新排列也不改变排列方式,
个篮子任意重新排列也不改变排列方式, 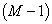 个篮子任意排列的方式有
个篮子任意排列的方式有  种。因此不同的排列方式有
种。因此不同的排列方式有
 (7.6.14)
(7.6.14)
种。将篮子后面球的个数看作一个态上的粒子数,则每种排列方式就都对应体系的一个状态。这样体系就有 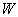 种可能状态。例如,有4个单粒子态,三个全同玻色子。则体系有
种可能状态。例如,有4个单粒子态,三个全同玻色子。则体系有
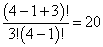
个可能的单粒子态。