§7.6
参考材料
定理2
若对全同粒子体系给定的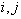 
满足
（7.6.15）
则对任意的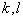 
亦有
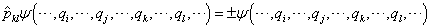（7.6.16）
证明：设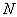 
个全同粒子体系的态矢量为
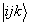（7.6.17）
其中，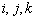 
为体系中任意三个粒子的坐标。规定狄拉克符号中三个粒子所处的位置依次为1、2、3。下面用反证法来证明上述定理成立。
首先，假设交换位于1和2位置的粒子是对称的，交换位于2和3位置的粒子是反对称的，则有
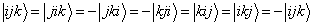（7.6.18）
显然，此时的波函数为零，故要求交换位于2和3位置的粒子亦是对称的。
其次，假设交换位于1和2位置的粒子是对称的，交换位于1和3位置的粒子是反对称的，则有
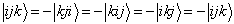（7.6.19）
显然，此时的波函数为零，故要求交换位于1和3位置的粒子亦是对称的。
由上面的结果可知，若交换任意一对粒子
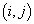时波函数是对称的，则交换与 
相关的其它粒子对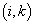 
、
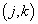时波函数亦是对称的。进而可知，交换 
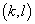粒子对也是对称的，其中， 
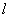为另外任意一个粒子。
同理可证，若交换任意一对粒子时波函数是反对称的，则交换其它粒子对时波函数亦是反对称的。
总而言之，全同粒子体系的波函数只能是对称的或者反对称的，不可能出现交换一部分粒子是对称的，而交换另一部分粒子是反对称的情况。