2. 自由玻色子与费米子性质的比较(曾谨言«量子力学教程§4.5.2»)
设有两个全同的自由粒子,都处于动量本征态.下面分三种情况讨论它们在空间的相对距离的概率分布.
(a)没有交换对称性.在不计及交换对称性时,两粒子的波函数可表示为
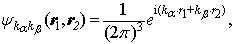(1)
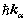与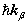
分别是粒子1和2的动量，令
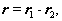
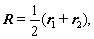
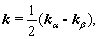
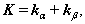(2)
r，R，
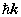和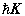
分别表示相对坐标，质心坐标，相对动量和总动量。式（2）之逆表示式为
，
，
，
. 
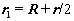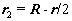
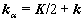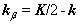（3）
于是式（1）可化为～.
对于粒子1和2交换，R不变，以下讨论略去与本题无关的质心运动部分。相对运动部分波函数为
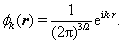（4）
这样，在距离一个粒子半径在（r，r+dr）的球壳层中找到另一粒子的概率为
（5）
式中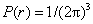
是常数（与r无关）。
（b）交换反对称波函数.当粒子
交换时，R不变，.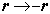
反对称相对运动波函数为
(6)
由此可以计算出
即
（7）
（c）交换对称波函数.类似可求出
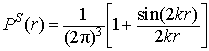（8）
令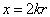
（无量纲），把三种情况下的相对距离的概率密度分布画于图7.4中。可以看出，在空间波函数交换对称的情况下，两个粒子靠拢的概率最大，而交换反对称情况下，两个粒子靠近（
）的概率趋于零，但当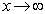
时，三种情况将无什么区别，.
此时，波函数的交换对称性的影响逐渐消失。从这个例子可以看出，全同粒子的相对距离的概率分布，与波函数的交换对称性有很密切的关系，这是一个可以观测的效应。
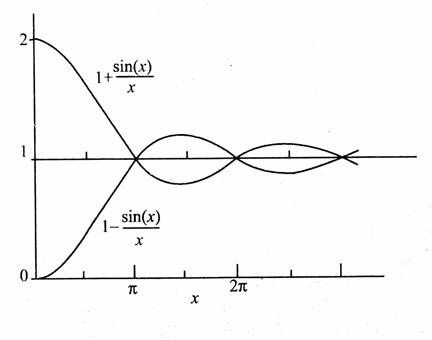
图7.4 三种情况相对距离的概率密度（引自曾谨言《量子力学教程》）