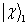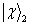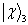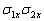3.纠缠态
由两个粒子组成的复合体系的量子态,如果能够表示为每个粒子的量子态的乘积,则称为可分离态。反之,称为纠缠态。例如,(7.4.16)-
(7.4.17)均为可分离态,这是可以理解的,因为(s1z
, s2z )
都是单体算符。而(7.4.18)-
(7.4.19)为纠缠态。
二体自旋算符力学量可选为

或等价的
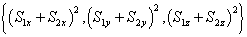
中的任二个,如
 。考虑到
。考虑到
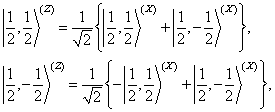 (1)
(1)
式中上角标
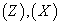 分别表示
分别表示 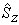 和
和 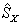 的本征态,可得到
的本征态,可得到 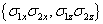 的
4个归一化纠缠态的基(贝尔(Bell)基)
的
4个归一化纠缠态的基(贝尔(Bell)基)
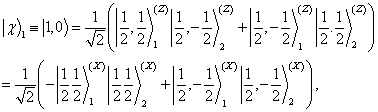 (2)
(2)
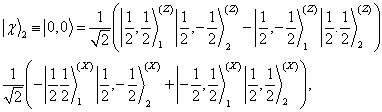 (3)
(3)
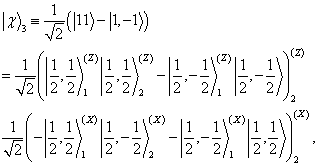 (4)
(4)
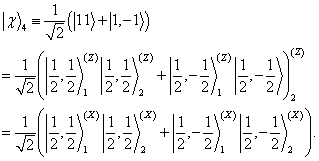 (5)
(5)
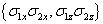 的
在这4个归一化的纠缠态上的本征值分别是
的
在这4个归一化的纠缠态上的本征值分别是
|
|
|
|
|
|
|
|
-1 |
-1 |
1 |
1 |
|
|
1 |
-1 |
-1 |
1 |
纠缠态一词是薛定锷在1935的一篇论文中给出的。同年,Einstein-Podolsky-Rosen(EPR)
的一篇论文对量子力学的正统诠释提出批评,就涉及纠缠态。Bell基于定域实在论的假设,研究了自旋为
 的二粒子体系的两个粒子的自旋沿空间任意两个方向a
和b
的投影的关联,得出了著名的Bell不等式。到20世纪80年代,Aspect
等人的实验结果,与Bell不等式相矛盾,证明量子力学理论预期的结果是正确的,而与玻姆等人的隐变量理论不一致。正对量子力学的正统解释(概率解释)是极大的支持。
的二粒子体系的两个粒子的自旋沿空间任意两个方向a
和b
的投影的关联,得出了著名的Bell不等式。到20世纪80年代,Aspect
等人的实验结果,与Bell不等式相矛盾,证明量子力学理论预期的结果是正确的,而与玻姆等人的隐变量理论不一致。正对量子力学的正统解释(概率解释)是极大的支持。
纠缠态的关联是一种纯量子的非定域的、超空间的关联,是量子态塌缩的非定域性在量子纠缠态中表现出来的奇妙性质。由(3)可看出,尽管两个粒子已经远离,对粒子1自旋态的测量仍然影响粒子2的自旋态。如果测得粒子1在
 态,则粒子2必在在
态,则粒子2必在在
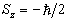 态;反之,如果测得粒子1在
态;反之,如果测得粒子1在
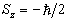 态,则粒子2必在在
态,则粒子2必在在
 态。即粒子2的状态取决于已经远离的粒子1状态的测量。
态。即粒子2的状态取决于已经远离的粒子1状态的测量。
理论上认为,纠缠态在可能的量子计算机和量子通讯中在有着极重要的作用,但迄今许多有关纠缠与非定域性的物理本质仍未得到最终的解决。
进一步可参阅《量子力学新进展》第一、二辑(北京大学出版社,2000,2001),第三辑(清华大学出版社,2003)中的有关综述性文章。