§7
进一步学习的内容
1.旋量的性质
在空间转动下,旋量的性质与标量.向量.张量完全不同。我们不作证明,仅以一例说明之。
定义算符
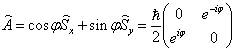
求解  的本征值及本征函数。求解过程从略。结果如下:
的本征值及本征函数。求解过程从略。结果如下:
本征值
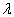 本征函数
本征函数
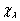
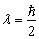
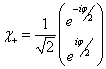
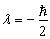

若作一空间旋转
 ,则
,则
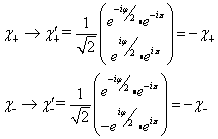
说明,在  时,
时, 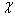 改变了一个符号,在
改变了一个符号,在 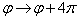 时,
时,
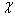 才回到原值。这就意味着,在
才回到原值。这就意味着,在  和
和 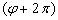 对应的空间同一点上,
对应的空间同一点上,
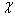 是双值的!这一点并不违背量子力学的基本原理,因为
是双值的!这一点并不违背量子力学的基本原理,因为 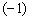 只不过是一相因子而已,而量子力学中的波函数本来就存在着相因子的不确定性。这也正是把自旋态矢称为旋量的原因。
只不过是一相因子而已,而量子力学中的波函数本来就存在着相因子的不确定性。这也正是把自旋态矢称为旋量的原因。
2.关于磁矩的公式
在本段将磁矩某些公式略作汇集。
1.
玻尔磁子
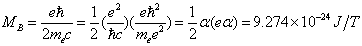
其中
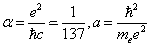
分别为精细结构常数和玻尔第一半径。 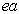 为原子电偶极矩的量度,因此
为原子电偶极矩的量度,因此  是原子磁偶极矩的量度。两者相差约两个量级
是原子磁偶极矩的量度。两者相差约两个量级

2.轨道磁矩
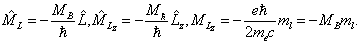
3.自旋磁矩

1.
对应任意角动量 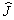 的磁矩
的磁矩
其中 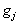 称为朗德(Lande)因子,它是反映物质内部运动的一个重要物理量。
称为朗德(Lande)因子,它是反映物质内部运动的一个重要物理量。
当 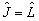 时,
时, 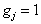 ;
;
当 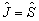 时,
时,  。
。