例题7.9
在口袋模型中,假设两个质量为 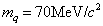 的夸克之间的相互作用为
的夸克之间的相互作用为
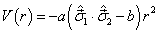
其中, 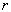 为两个夸克之间的距离,
为两个夸克之间的距离, 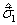 与
与 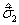 分别为两个夸克的泡利算符,作用强度
分别为两个夸克的泡利算符,作用强度 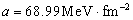 ,问当
,问当 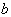 取什么值时,才能使得两个夸克束缚在一起。
取什么值时,才能使得两个夸克束缚在一起。
解:若令两个夸克的总自旋算符为
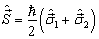 (1)
(1)
则位势可以改写成
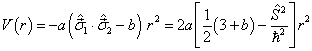 (2)
(2)
体系的哈密顿算符为
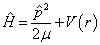 (3)
(3)
式中, 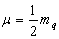 是两个夸克的折合质量。由上述两式可知,力学量的完全集为
是两个夸克的折合质量。由上述两式可知,力学量的完全集为 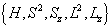 ,波函数可以写成空间部分与自旋部分的乘积形式,即
,波函数可以写成空间部分与自旋部分的乘积形式,即
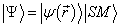 (4)
(4)
在上述状态之下计算哈密顿算符的平均值
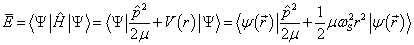 (5)
(5)
式中,
 (6)
(6)
显然,(5)式中的算符就是球谐振子的哈密顿算符,只不过是角频率与总角动量的量子数 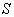 有关而已,欲使其有束缚态解,则要求
有关而已,欲使其有束缚态解,则要求
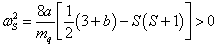 (7)
(7)
或者
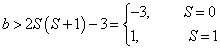 (8)
(8)
所以,两个夸克形成束缚态的条件为
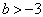
例题7.10
两个自旋为 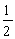 的全同粒子,同处于宽度为
的全同粒子,同处于宽度为 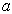 的非对称无限深势阱之中,若两粒子之间的相互作用可以忽略,求体系的基态与第一激发态的能量和波函数。
的非对称无限深势阱之中,若两粒子之间的相互作用可以忽略,求体系的基态与第一激发态的能量和波函数。
解:非对称无限深势阱的解是已知的,由于 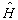 与自旋无关,所以单粒子的本征值及本征态是
与自旋无关,所以单粒子的本征值及本征态是
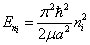
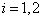 (1)
(1)
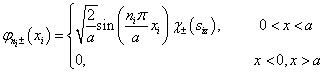 (2)
(2)
式中,第![]() 个粒子的磁量子数
个粒子的磁量子数 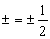 。
。
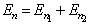 (3)
(3)
对于基态而言, 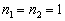 ,
,
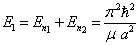 (4)
(4)
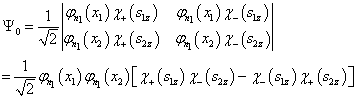 (5)
(5)
对于第一激态,  ,
,
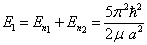 (6)
(6)